6
CF1826F
交互。笛卡尔坐标系下有n<=25个点,每次询问你可以给一条直线,交互会告诉你所有点在这条直线上的投影坐标(打乱顺序)。在最小询问次数下还原所有点。50组多测。所有点的x、y坐标至少相差1,交互给投影坐标的时候会加入0.0001的噪音(所给点和实际点的距离小于等于0.0001)。答案与实际答案的距离在0.001范围内算通过。
显然问两次不行,显然问三次可以。首先问两次两条坐标轴,然后会得到\(n^2\)个备选点。之后随机一条直线,判断这条直线能否让这些备选点两两的投影不同。应对噪音只需要把eps设大一点就可以了。可以设为0.0008左右。
CF1726H
我草,随机开题开出来个阴间玩意儿
给一个凸包。一个点被染红当且仅当存在一条长度不超过1的凸包的弦经过该点。弦的端点可以在凸包的边上。求红色区域面积。凸包5000个点,坐标正负1e9内。
CF1578F
要用一个面积最小的长方形覆盖住一个凸包(n<=2e5),但是长方形的角度未定。现在角度随机分布,求这个长方形面积的期望。
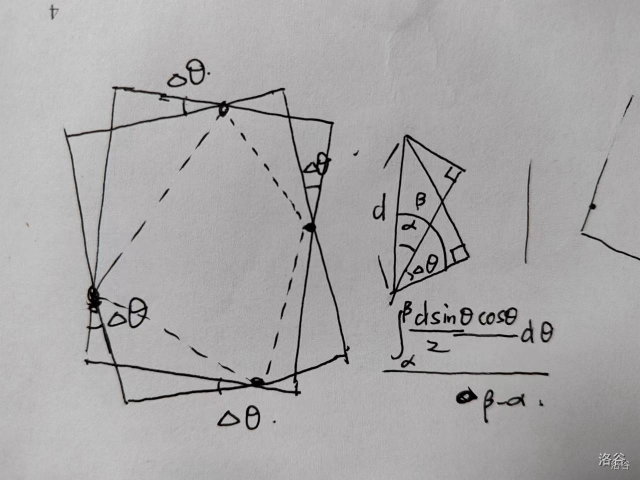
先跑旋转卡壳,把\(2\pi\)划分成\(O(n)\)段,每段\(\Delta\theta\)内,限制四条边的顶点相同
然后是一个简单的积分
CF1578I
交互。有一个圆心坐标都在正负1e5内,半径也在1e5内的圆,保证原点在此圆外且原点到此圆的距离至少是1。每次询问你可以给出一条从原点出发,经过\((x_q,y_q)\)的射线,交互器返回圆到射线的距离(定义为圆和射线上分别找一点的最近距离)。其中你给出的\(x_q,y_q\)必须都是正负1e6内的整数。60次询问内猜出圆心坐标和半径。保证圆心坐标和半径都是整数(因此没有精度spj)
首先先各询问一遍4个坐标轴方向。其中最大的那个一定是原点到圆的距离。接着如果最小的一个不是0,那直接出答案。如果最小的一个或者两个都是0,那么需要进一步操作。
假设不限制询问必须是整数,我们直接从4个坐标轴最大的那个开始往两边二分,把切线二分出来,结合原点到圆的距离就能算出圆心半径和坐标
限制是整数的话我们就把正负1e6边界上总共8e6个点拿来二分。注意到这样的话,能用的角度就是离散的了,但是没关系。我们把最靠近切线的角度拿出来,不难发现由于1e6比圆心坐标范围1e5大一个数量级,二分出来的两条最靠近切线的"亚切线"的角度一定在圆心所在的那个半平面内。这样我们还是能结合原点到圆的距离算出答案。
CF198C
原点处有一个半径为r的定圆,同时有一个动点以R为半径绕原点做匀速圆周运动,线速度已知,初始位置已知。R>r。有一只蚂蚁初始时在定圆外位置已知,蚂蚁的速度已知,求蚂蚁追上动点的最短时间。保证蚂蚁的速度大于动点的线速度。蚂蚁不能进入定圆内。
由于保证蚂蚁的速度大于动点的线速度,所以可以二分答案。假设二分的答案是mid,那么可以求出动点的末位置,然后计算蚂蚁的初位置到动点的末位置所需的时间。简单讨论一下:如果两点间构成的线段到原点的距离大于等于r,就是两点间距离,否则是两段切线加一段圆弧。
Gym100801(NEERC15~16)K
给一条折线段\(P_1\to P_2\to ...\to P_n\),现在需要简化这条折线段为\(P_{i_1}\to P_{i_2}\to ...\to P_{i_m}\),其中\(1=i_1<i_2<...<i_m=n\),且\(\forall k\in[1,m-1],\forall j\in [i_k,i_{k+1}],P_j\)到线段\(P_{i_k}P_{i_{k+1}}\)的距离不超过给定的d。求出最小的m。n<=2000。
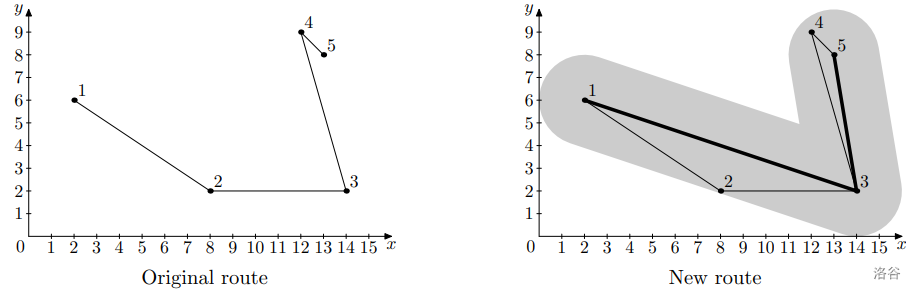
考虑dp。dp[i]表示考虑前i个点,要求第i个点必须选的答案。那么转移就枚举上一个点j。考虑从i-1倒着枚举j,同时维护一个可行角度,只需要保证\(P_j\)在\(P_i\)到\(P_{j+1},...,P{i-1}\)的可行角度范围中即可。
维护可行角度时,考虑用\([\theta,\theta+\Delta\theta]\)维护,避免使用\([\theta_L,\theta_R]\)。前者能避免一些讨论。
Gym101234(16~17台国立wf选拔)H
给定严格在第一象限的封闭多边形。求一条过原点的直线将这个多边形划分成尽可能多不连通的部分。多边形按照逆时针方向给出。1e5个点。
下图答案是5
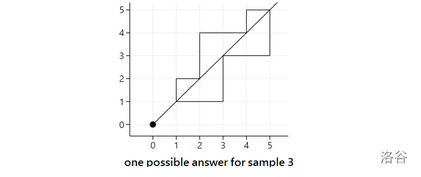
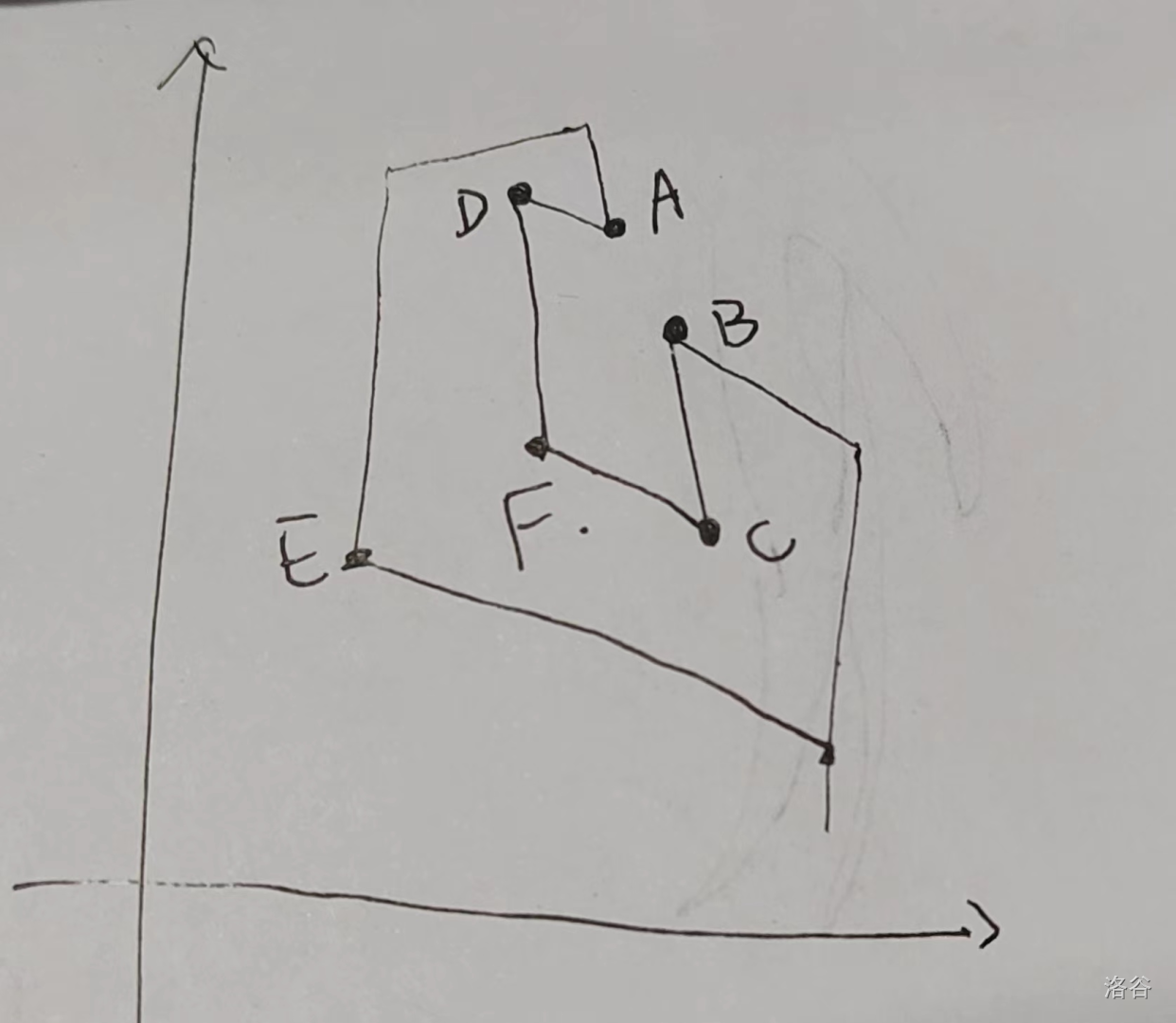
考虑把所有点极角排序,然后扫描线。把所有点分为“碰到这个点就立刻改变”、“碰完这个点再改变”、“不改变”三种。
下图中,BC是碰到这个点就立刻改变”,AD是“碰完这个点再改变”,EF是“不改变”
Gym101790B
给出n(1e5)个笛卡尔平面上的点,你可以再平面上任意取一个点,然后把这n+1个求凸包。求这个凸包的最小点数-1。如果凸包上的某条线段经过了一个点,那么这个点也算是凸包上的点。

新加的点必然是加在无限远处最优。因此跑一个原图的不严格凸包,然后旋转卡壳,答案是半个“壳”的大小。注意特判平行的情况。
Gym100801(14~15icpc东京)H
你操作一个圆形机器人,要从出发点运动到目的地。平面上有一些洞(抽象为点),你不能让机器人经过洞(点可以在圆上但不能跑到圆内)。洞小于等于8个。
这题勾起了我不好的回忆...我写过这题加强版,n<=300。
首先圆绕过点改成点绕过圆。即,你操纵点在平面上运动,不能进入给定的圆内。然后发现点走的路径一定是一些圆弧和圆与圆之间的切线。因此两两枚举圆,计算切线,把切点也标记到圆上,然后切线建图,同一个圆的切点之间建图,切线建图时需要保证线段与所有圆都不交。然后得到点和边都是n^2级别的图,跑dijkstra。
非常tmd难写,注意细节。
HDU4785
给定一个长方形的房间,房间的边平行于坐标轴,房间内有一个扫地机器人,机器人的形状是一个凸包。房间内还有一些家具,家具也是凸包。扫地机器人可以在房间内随意平移(不能旋转),可以穿过家具,但是只有当机器人不和任何家具有交时才能扫地。扫地机器人并非覆盖到的点都能清扫,而是只有凸包上的第一个点能清扫。求能清扫的范围大小。至多20个家具,每个(21个)凸包至多20个点。
最开始没看到机器人不能旋转,想了好久。考虑一个家具带来的实际障碍作用,发现是家具凸包和机器人反凸包的闵可夫斯基和。那么答案就是一个长方形内没有被这些闵可夫斯基和覆盖的点。扫描线即可。点很少,怎么暴力怎么来就好。
2023牛客多校1B
给一个凸包,在凸包上找三个点,满足:这三个点构成的三角形的反互补三角形完全覆盖此凸包。如果ΔABC三遍中点分别为X,Y,Z,则称ΔABC是ΔXYZ的反互补三角形。凸包1e6个点。
如果固定三个点中的两个,不难发现第三个点至少必须满足:它到两固定点所在直线距离最大。因此,定下两个点,第三个点就定了。因此实际上只有两个动点。跑这两个动点的双指针就行了。
CF1584G
给定\(n\)个互异的点\(p_1\sim p_n\),求有多少对\((i,j),i< j\)满足对于所有的\(k\in [1,n]\),\(p_k\)到线段\(p_i,p_j\)的距离小于等于给定的\(R\)。\(n\le 3000\)。
智慧题。先来一个神仙转化:\(p_k\)到线段\(p_i,p_j\)的距离小于等于\(R\),当且仅当\(p_k\)到射线\(p_i,p_j\)的距离小于等于\(R\)且\(p_k\)到射线\(p_j,p_i\)的距离小于等于\(R\)。
枚举一个\(i\),现在考虑一个\(k\)。从\(p_i\)向以\(p_k\)为圆心,\(R\)为半径的圆引两条切线产生一个夹角,设这个夹角为\(A_k\),那么\(p_j\)只能落在\(A_k\)里面。(如果\(p_i\)在圆内部,那么不产生限制,continue掉)现在把所有\(p_k\)产生的夹角求交,\(p_j\)只能落在交里面。枚举一遍\(k\)再枚举一遍\(i\)就行了。
CF1575M
小清新凸包题
有一共\((n+1)(m+1)\)个点,横纵坐标分别是\([0,n],[0,m]\)之间的整数。有一些点是特殊点,用\(n+1\)个长度为\(m+1\)的01串告诉你。设\(S(x,y)\)表示距离\((x,y)\)这个点最近的特殊点的欧氏距离的平方。求所有点\(\sum S(x,y)\)。
固定\(y\),考虑某个特殊点\((x_k,y_k)\)的贡献,是\((x-x_k)^2+(y-y_k)^2\) \(=x^2+(-2x_k)+[x_k^2+(y-y_k)^2]\)。\(x^2\)是对于每个\(x\)固定的贡献,可以最后加,定住\(y\)的话方括号里的东西是关于\(k\)固定的。那么令\(A=-2x_k,B=x_k^2+(y-y_k)^2\),现在就是有很多对\((A,B)\),要对每个\(x\)求\(Ax+B\)的最小值。可以用凸包解决。注意\(x_k\)相同的特殊点只需要拿出来一个,所以固定\(y\)的话\((A,B)\)只有\(O(n)\)对。又注意到,\(A\)是天生单调的,建凸包不用排序,求最小值直接把\(x\)用个指针扫,整个过程是不带\(\log\)的。
CF1575B
小清新套路题
平面有\(n\)个点,你需要画一个经过原点的圆覆盖至少\(k\)个。问你所需要的最小半径。
二分答案,每个点对应一个角度区间,套路离散差分一下就行。写一下练下手。
这种二分的题很香,写的时候完全不用考虑eps之类的杂七杂八的问题,毕竟二分,大一点不行小一点总行。
看了看题解发现这题卡常,可能需要先二分答案的第一个非零数字,然后再常规二分。幸好正常写也过了。
CF592E
思路很简单,写出来特别难受的题。这个题卡精度,double和long double都过不了,极角排序必须用atan2和叉积混合判断。
平面上有\(n\)个坐标,对于两个坐标\((x_1,y_1),(x_2,y_2)\),如果有\(x_1y_2-x_2y_1>0\),连接一条单向边。求三元环的个数。
这个判定的形式是一个叉积,很自然地考虑几何意义。三元环的几何意义就是按照顺序,三个点的角度差都小于\(\pi\)。因此,可以考虑枚举其中的一个点,假设这个点的犄角是\(\theta\),那么第二个点的极角\(\varphi\)必须在\((\theta,\theta+\pi)\)之间,第三个点的角度\(\gamma\)必须满足\(\gamma+\pi\in(\theta,\gamma)\)。考虑提前把第三个角加上\(\pi\),然后一对\((\theta,\varphi)\)的贡献就是一个区间和,直接求前缀和做差。那么所有\(\varphi\in(\theta,\theta+\pi)\)的贡献就是前缀和的前缀和。
需要注意精度问题。极角排序的时候,两个点先求极角,如果极角的差比较大(比如,大于\(\frac{\pi}2\)),直接比较极角大小,否则用叉积判断。unique的时候也要用叉积去重。