6
本来周日晚上打算补题,但是想到补题可以课上补,五个小时的空闲平时难找,然后就开了场NEERC。
ADM
签
K
给一个n1e18,求最少拆成几个二进制下111...1这样的数的和,再减1。比如n=5=1+1+3,答案是3-1=2;n=6=3+3,答案是2-1=1,n=19=15+3+1,答案是3-1=2。
枚举答案,然后每次搞的是二进制的11...1,加个1变成100...0,算一下popcount
J
n2e5只青蛙在数轴上,一开始坐标是\(a[1...n]\),一小会之后变成了\(b[1...n]\),所有青蛙完全等价不可区分,2n个坐标互不相等。问往左跑的青蛙有多少只?输出所有可能的答案。
首先答案是连续段,求最小和最大可能就行了。
对于最大,肯定是牺牲\(a[1...i]\)向右去到\(b[n+1-i,...,n]\),然后看看腾出来的位置够不够让后面的都往左,能就记录答案。枚举这个i就行。
对于最小,那就是让向右跑的尽可能多。把a[]b[]交换,再求一边最大,用n减掉就行。然后输出最小和最大之间的所有数。
G
给n500,p<=n,求有多少种n-p的拆分使得拆分中的数异或起来等于p。拆分不同当且仅当拆分构成的multiset不同。
dpik表示和为i,最大是j,异或和是k,即可。然后每次加一个j,可以前缀和优化。
看起来空间很爆炸,\(n\times n\times(2n)\),但是实际上k那一位 不用开\(2n\),开到\(511\)就够了
。
最开始想错了,40min才过。
E
n2e5个国际象棋的皇后摆在值域为±1e8 的坐标系上,他给的皇后坐标互异,找一个位置摆一个皇后能攻击到所有皇后。规定皇后可以重叠:你摆的皇后可以和某个皇后坐标相同。
可以结合unordered_map、unordered_set O(1)check一个位置是否可行。然后注意到潜在的可能ok的位置只有O(n)个:枚举所有可能的横竖线和斜线,随便拎一个皇后(比如(x[1],y[1])),这个皇后会在枚举的横竖线或斜线上确定至多3个预备位置。check下就好。
常数大概就有一个多的log,如果不用unordered会T。用unordered也要先count再[],不然也T。
中间这个题卡了快两个小时,干了9发才过。中间还去尝试自己写hashmap,结果因为忘考虑负数,re到怀疑人生。
I
交互题。有n<=10个格子排一行,有\(n(n+1)/2\)个挡板,每个挡板能覆盖\([i,j]\)的格子(刚好n(n+1)/2个)。你不知道这些挡板中哪些开哪些关,但你可以开关这些挡板(改变状态)。每次改变后交互会告诉你有几个格子没有被任何挡板覆盖。目标是关闭所有挡板,也就是某次操作后如果交互机返回n就算成功。
先干一边n位格雷码,把第n个格子干开(第一次有新的未覆盖格子的时候要检查下\([1,n-1]\)这个挡板开没开,没开要开上,以免干扰我们干第n个格子)。然后继续格雷码往下干。格雷码递归构造。
F
你有一个栈,栈内存放了一些有颜色的球,最开始空。现在告诉你出栈球的颜色序列和入栈球的颜色序列,长度都是n100,要用一个仅包含SC两个字母的、长度2n的串表示栈的操作序列。
区间dp。\(dp[i][j][a]\)表示入栈序列的[i,j]能不能跟出栈序列的[a,a+j-i]匹配上。转移枚举入栈序列第一个球跟出栈序列哪个位置匹配,匹配要那两个球颜色相同,并且中间和后面都能匹配。方案递归dp完了找回去构造。
接下来是补题。这场没有hard都是med-hard,所以可以看到好几个队ak了
B
智商题。
给你一个n1e18,求n在哪些进制下0的个数最少?输出0的最小个数以及所有能达到这些答案的进制,比如11在二进制、三进制、十一进制下都只有一个零。T1000组数据。
首先考虑到这个题答案肯定不会很小。如果一个数在二进制下0很少,三进制下不一定很少,这些进制看起来是随机的。考虑一个暴力算法:一个一个从二进制开始枚举进制,如果枚举到后面位数不够永远超不过现在已经枚举到的最大答案了就break掉。然后这个算法会T掉,但是如果加上了记忆化就能过了。
上面的做法看起来很智慧,但是题目给了正确性的证明。首先他证明了0的最小个数小于等于4的情况很少:我们在本地打表大于4096并且二进制小于等于4个0的所有数字,大概有百万级别个,然后再本地跑上面那个暴力算法,跑出来超过4096且答案小于等于4的数字只有16 760 831, 6143, 14335, 262079, 262111,524 031,524 285这几个,把几个打表。然后其他的要么本身小于等于4096,要么因为\(4096^5\ge1e18\),枚举的复杂度不超过4096,1000组数据可以过。如果没有做以上的分析,无脑稀里糊涂的记忆化也能过就可以理解。
C
给定一个大小为2n(n1e5)的树,树上每个点有一个颜色,每种颜色恰有两个点。也就是刚好有n种颜色。现在要从这个2n的树上选一个大小为n的连通块,恰包含n种颜色每两个种的一个节点。
这个题比F简单点?不觉得。主要是有个很显然但是不容易注意到的key observation:从大小2n的树上选n个点的连通块,那么块上至少有一个点是树的重心。那么先枚举重心为书的根,假定重心一定要选,然后就可以跑2-sat:一个点选推出父亲选,推出同色点不选。跑出来之后随便取一个方案即可。
L
题意不好阐述,链接Problem - L - Codeforces.
这个题需要手玩。补题的时候感觉不难,后面自己切掉了。不知道题解做法是不是这样。
这个题要一行一列一个一个地填数。我们先不管整数的限制,允许填浮点数。等填完了所有数之后离散化到范围内就可以。
第一行相对大小可以随便定,假设先填1~m
之后的每一行的第一列先随便填(一个跟之前的数都不一样的数),然后剩下的\((i,j),i>1,j>1\)的位置就需要解决:知道\((i-1,j-1),(i-1,j),(i,j-1)\)填的数是什么,需要决定\((i,j)\)填什么。实际上手玩可以发现,无论哪三个位置的相对大小长成什么样子,\((i,j)\)总能找到符合条件的填法。因为现在填的是浮点数,可以随意在中间插入值。于是就可以一个一个填下去。
然后问题是浮点数精度不够,n500m500,浮点数经不住500次取中间值(其实我没写,不是很确定够不够,但是八成不够)。因此可以考虑用平衡树代替浮点数,每次取那三个位置在平衡树上的rank,然后按照相对大小把\((i,j)\)插入平衡树对应位置。
H
若至几何题,补题没做出来。有点对不起之前练的几何。
给定两个定点P和Q(坐标±1e9),和n2e5条线段。两条线段a, b能和P、Q构成H形状当且仅当:
P严格在a内,不能在端点上。a和线段PQ不平行。
Q严格在b内,不能在端点上。b和线段PQ不平行。
a、b严格不交
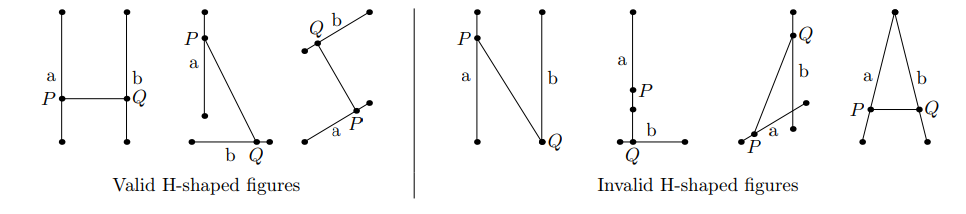
求PQ和这些线段能形成多少个H形状。
首先把平行于PQ的线段扔了,然后严格包含P的归入集合\(A\),严格包含Q的归入集合\(B\)。显然\(A\cap B=\varnothing\)。然后求\(A,B\)中的线段有多少对相交的,假设有\(I\)对,答案就是\(|A|\times|B|-I\)。然后考虑求\(I\)。注意到\(A,B\)中的线段可能在线段\(PQ\)上方相交,也可能在下方相交,但不会同时在上方和下方相交。所以上下方可以单独算。假定在上方相交,那么把\(A,B\)中的线段在\(PQ\)上方的点取出来,考虑相交的条件:假设\(R\)是\(A\)中某线段的端点,\(S\)是\(B\)中某线段的端点
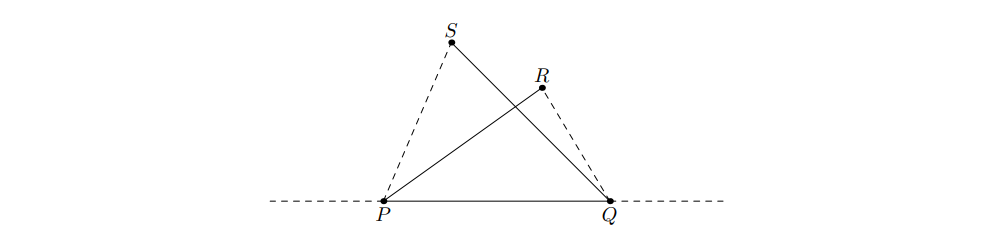
那么∠RPQ<∠SPQ,∠RQP<∠SQP。这就是一个二维偏序问题,可以用树状数组解决。
注意这个题卡精度,double卡不过,但是long double运气好能卡过。最好这个题中间不要有任何角度信息,中间的所有比较都用外积算。包括lower_bound也写一个比较器。