123
A
考虑最终序列 \(b\) 需要满足什么条件,若 \(b_i>b_{i+1}\),那么至少需要在 \(i\) 这个位置上做 \(b_i-b_{i+1}\) 次前缀加操作,于是总共至少需要做 \(\sum_{i=1}^{n-1}\max\{0,b_i-b_{i+1}\}\) 次前缀操作,为了方便,在开头末尾添加两个足够大的元素 \(b_0,b_{n+1}\) ,满足 \(b_0=M\geq \sum_{i=0}^{n}\max\{0,b_i-b_{i+1}\}\) 。
注意到满足 \(\sum_{i=0}^n\max\{0,b_i-b_{i+1}\}=\sum_{i=0}^n\max\{0,b_{i+1}-b_{i}\}\) ,于是可以把限制相加得到 \(\sum_{i=0}^n|b_i-b_{i+1}|\leq 2M\) 。原问题中代价综合为 \(b\) 的和,于是考虑将问题转化为可以花1的代价将 \(a_i\) 加1,最少代价满足上述限制。
显然贪心即可,每次选择一段极长相等段 \(a_l=a_{l+1}=\dots=a_r,a_{l-1}>a_l,a_{r+1}>a_r\),将所有元素加1可以使总和减2,考虑建笛卡尔树,每次贪心选择长度小的相等段即可。
F
给你一棵树,一个 1 到 n 的排列 p 和一个常数 K。q 组询问,每次问排列中的一个区间 \(p_l, p_{l+1}, \dots , p_r\),这些点 K-邻域的并的大小。\(nK ≤ 2 \times 10^6, q ≤ 5 \times 10^5\)。
离线询问,顺序枚举询问右端点 \(r\) ,维护数组 \(lst\) ,对于每个点 \(u\),令 \(lst_u\) 为最大的 \(x\leq r\) 满足 \(u\) 在 \(x\) 的K-邻域中。
考虑如何维护 \(lst\) 数组,考虑bfs序,每次加入一个点时,实际上是在对 \(2K+1\) 段赋值,用set维护区间,bit维护后缀和回答询问即可。
K
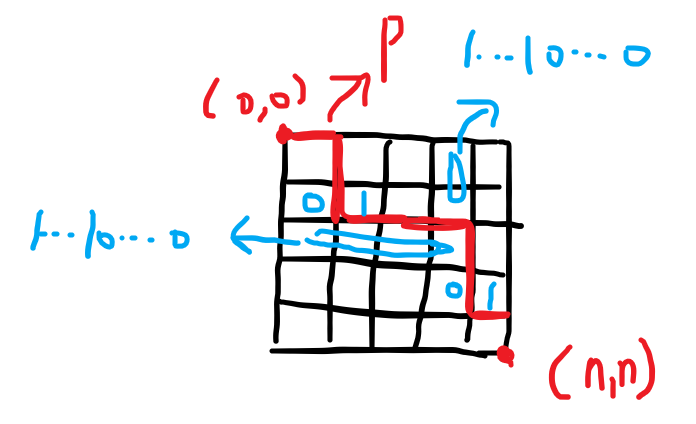
考虑一个合法矩阵 \(A\),一定可以找出一条从格点 \((0,0)\) 走到格点 \((n,n)\) 的路径 \(P\),使得所有横木棍在 \(P\) 左下,竖木棍在 \(P\) 右上。由于要对合法矩阵 \(A\) 计数,故我们试图让 \(A\) 与某个 \(P\) 一一对应,考虑最右上的合法的 \(P\),那么最右上的条件是什么呢?
如图所示,在一个下右转角处,必须是 01 才能令 \(P\) 不能继续往右上,而其他位置则没有特殊的限制,于是可以考虑 dp,令 \(f_{i,j,0/1}\) 表示当前走到了格点 \((i,j)\) 上一步是向右/下时的合法方案数。考虑总共 4 种移动方式,可得转移:
\[ \begin{cases} f_{i,j,0} \cdot b_{i,j+1} \to f_{i,j+1,0} \\ f_{i,j,0} \cdot a_{i+1,j} \to f_{i+1,j,1} \\ f_{i,j,1} \cdot c_{i,j+1} \cdot \frac{a_{i,j-1}\cdot [s_{i,j} \neq '1']}{a_{i,j}} \to f_{i,j+1,0} \\ f_{i,j,1} \cdot a_{i+1,j} \to f_{i+1,j,1} \end{cases} \]
其中 \(a_{i,j}\) 表示第 \(i\) 行到了 \(j\) 是 1...10...0 的方案数;\(b_{i,j}\) 表示第 \(j\) 列到了 \(i\) 是 1...10...0 的方案数;\(c_{i,j}\) 表示第 \(j\) 列到了 \(i\) 是 1...1 的方案数。
M
考虑一个没有 ? 的串如何计算答案,模拟球滚动的过程,从前往后扫,类似于一个栈中存放 >,遇到 > 入栈,遇到 < 出栈并计算贡献。
考虑 dp,设 \(f_{i,j,0/1}\) 表示当前考虑到了 \(i\),栈中还有 \(j\) 个 >,或往后借了 \(j\) 个 <,求最后为 >/< 时的最大贡献球数量(包含栈中的球)。每次加入一个 > 时就将其压入栈,转移为 \(\max\{f_{i,j,0},f_{i,j,1}\}+1 \to f_{i+1j,0}\) ;每次加入一个 < 时若上一个为 < 且栈中有 > 则出栈,转移为 \(f_{i,j,1}+1 \to f_{i+1,j-1,1}\) ;若上一个为 >,此时会产生损耗,有3种不同的操作,当前为 >>>< 可以将其变为 >>>,>>,> 其中的一个,于是枚举 \(p \in [0,2]\),转移 \(f_{i,j,0} \to f_{i+1,j-p,1}\) 。
最后在计算答案时将在栈中未处理的 > 减去即可。