眼瞎
K
场上有点弱智了呵呵,,,,,
题意,给一个坐标系,然后原点有个光源,x坐标为正的半区有很多(n<=3000)垂直的挡板,不包含不相交。然后比这些挡板x坐标更大的某处(显然具体坐标是多少不重要)有一个投影屏幕。现在把光源沿x轴负方向移动,速度1单位/s,问有多少时间中,影子连成完整的一片。无穷输出-1。
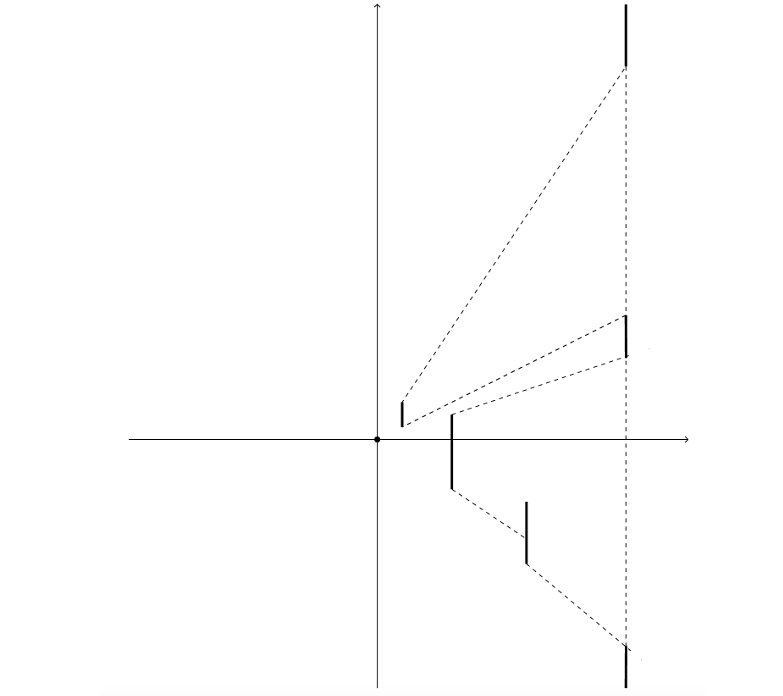
要让整个影子连成一片,其实就是从光源这里看隔板,隔板连成一片,中间看不到投影屏。也就是,去看每个挡板的两端点,然后把俯仰角排序,任意前缀中,下端点对应的俯仰角更多。据此可以把端点两两连线,求出他们排位改变的地方共\(O(n^2)\)个,然后扫。每个地方涉及一个交换,交换的同时要维护任意前缀是不是都是下端点更多。这个可以通过把下断点看成1,上端点看成-1,然后求前缀和,记录有多少个0,来\(O(1)\)实现。
细节有点麻烦,最难受的是出现三点共线的情况。出现这种情况可能会出现同时有多个点的排名发生变化,但是由于对交换事件排序的不当,正要交换的点并不相邻的情况。为了解决这样的问题,需要把交换事件的排序加入y坐标作为排序关键字,这样按顺序一个一个的交换就不会出现上面构式的情况。