123
H
写的线性做法不是题解的那个,题解那个有点智慧
把每个个点按照那\(k\)个矩形的覆盖情况着色并划分为连通块。如果一个连通块(覆盖情况相同,由相同集合的矩形覆盖)是某些矩形的交,需要:
是矩形。可根据面积和最大最小坐标判断
四个方向都有向内的边。可根据输入的矩形提前利用差分放到一张表格上
只需要差分和dfs或者之类的东西跑连通块,\(O(mn+k)\)
F
atc风格鲨我

\(k\le n+m\le 5\times 10^6\)
首先需要观察出抽象结论:双倍币一定是在最后k场,每场开始前根据余下胜负场数判断要不要用。原因:假设只有一枚币,如果我们必须在比赛之前决定在哪一场一定要用,那么选任意一场都一样,因为每一场的概率都是均匀的。但是我们可以根据比赛情况决定是否使用。如果我决定在某一场使用,但是由于就当前情况看,下一场的期望和这一场是一样的,并且下一场可以知道这一场的输赢,下一场的视角更加清晰,不如把币留给下一场。以此类推如果只有一枚币一定是留到最后一场使用最好。类似可以用归纳法证明,如果有k枚币,一定是最后k场使用。
那么我们发现最后k场每次用不用是独立的,直接单独计算额外得分的期望。枚举最后的第\(i(i\le k)\)场,其中有\(p,q(p+q=i)\)场胜/负。那么
\[ \begin{aligned} Ans&=\sum_{p+q=i\le k}\frac{\binom{p+q}q\binom{n-p+m-q}{n-p}}{\binom{n+m}m}\max(\frac{p-q}{p+q},0) \newline &=\sum_{p+q\le k,p>q}\frac{\binom{n-p+m-q}{n-p}}{\binom{n+m}m}(\binom{p+q}q\frac p{p+q}-\binom{p+q}q\frac q{p+q}) \newline &=\sum_{p+q\le k,p>q}\frac{\binom{n-p+m-q}{n-p}}{\binom{n+m}m}(\binom{p+q-1}{p-1}-\binom{p+q-1}p) \end{aligned} \]
这个式子应该做法很多,但是我看题解和zky的代码都看不懂,最后看HoMaMa的看懂了,就写一下他们的做法。把分母提出来,把减号拆开,并且为了方便,记\(path(x,y)=\binom{x+y}{x}\)。先看前一半
\[ \begin{aligned} &\sum_{p+q\le k,p>q}\binom{n-p+m-q}{n-p}\binom{p+q-1}{p-1} \newline =&\sum_{p+q\le k,p>q}path(n-p,m-q)path(p-1,q) \newline =&\sum_{p+q\le k-1,p+1>q}path(n-1-p,m-q)path(p,q) \end{aligned} \]
考虑组合意义:这就是要对于每个满足\(p+q\le k-1,p+1>q\)的点\((p,q)\)计算,有多少条从\((0,0)\)到\((n-1,m)\)的路径经过它。把这片区域画到坐标系上去, 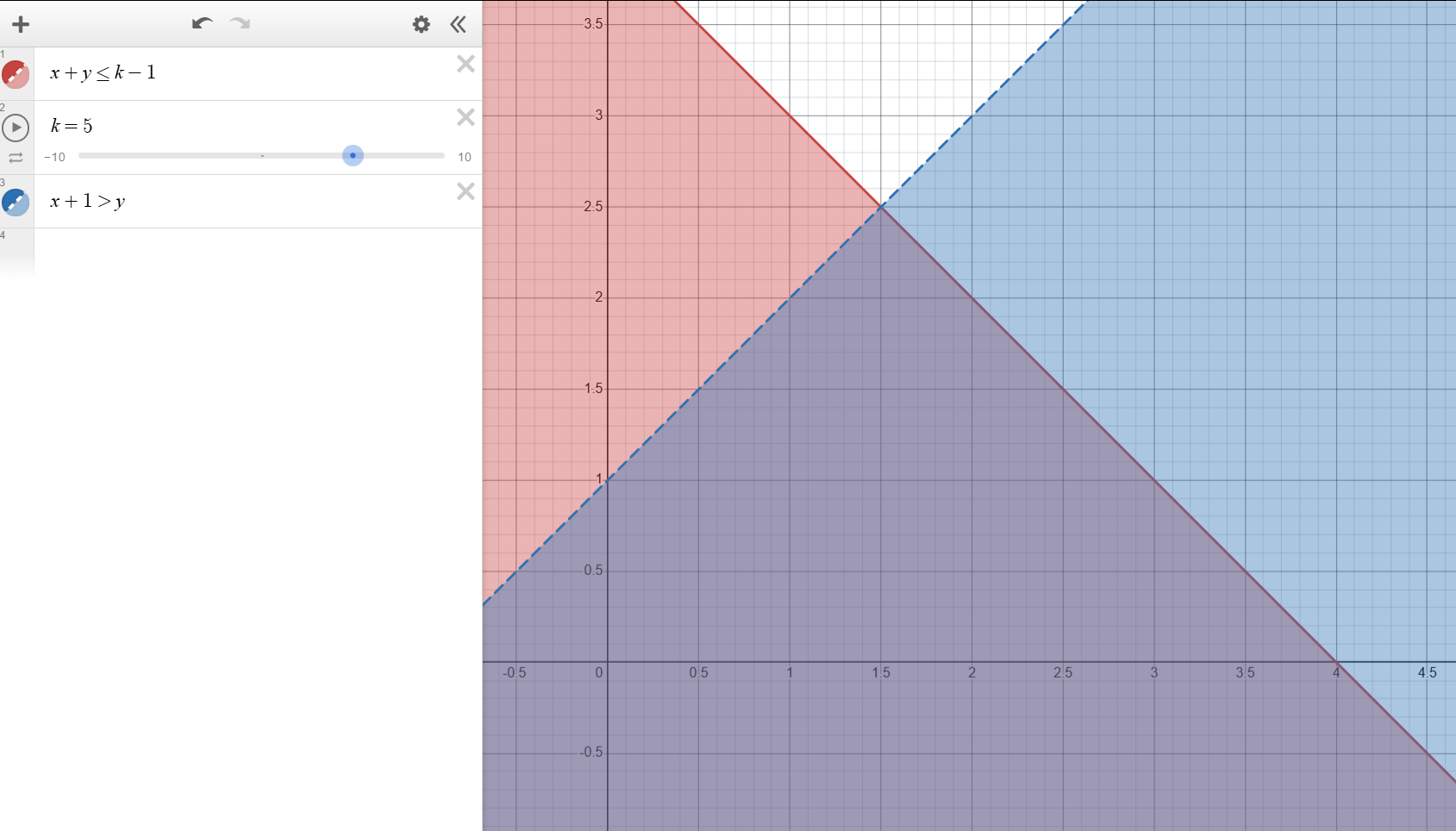
可以考虑把相同\(i=p+q\)的\((p,q)\)一起算。具体的,枚举从小到大\(i=p+q\),记录一个计数器\(cur\)表示\(i=p+q,p+1>q,p\ge 0,q\ge 0\)这条线段上的\(path(n-1-p,m-q)path(p,q)\)之和是多少。初始\(i=0\)时\(cur=path(n-1,m)\)。如果把所有可能的从\((0,0)\)到\((n-1,m)\)的路径画到图上,\(cur\)记录的就是\(i=p+q,p+1>q,p\ge 0,q\ge 0\)这条线段上的路线插头的数目和。那么迭代\(i\)的时候,就根据\(i\)的奇偶性,考虑有没有从\(p+1>q\)上方进来的新插头或者有没有从下方跑上去的插头,更新\(cur\),并累加到\(Ans\)上就可以了。下图红色的是进来的插头,黑色是出去的插头。
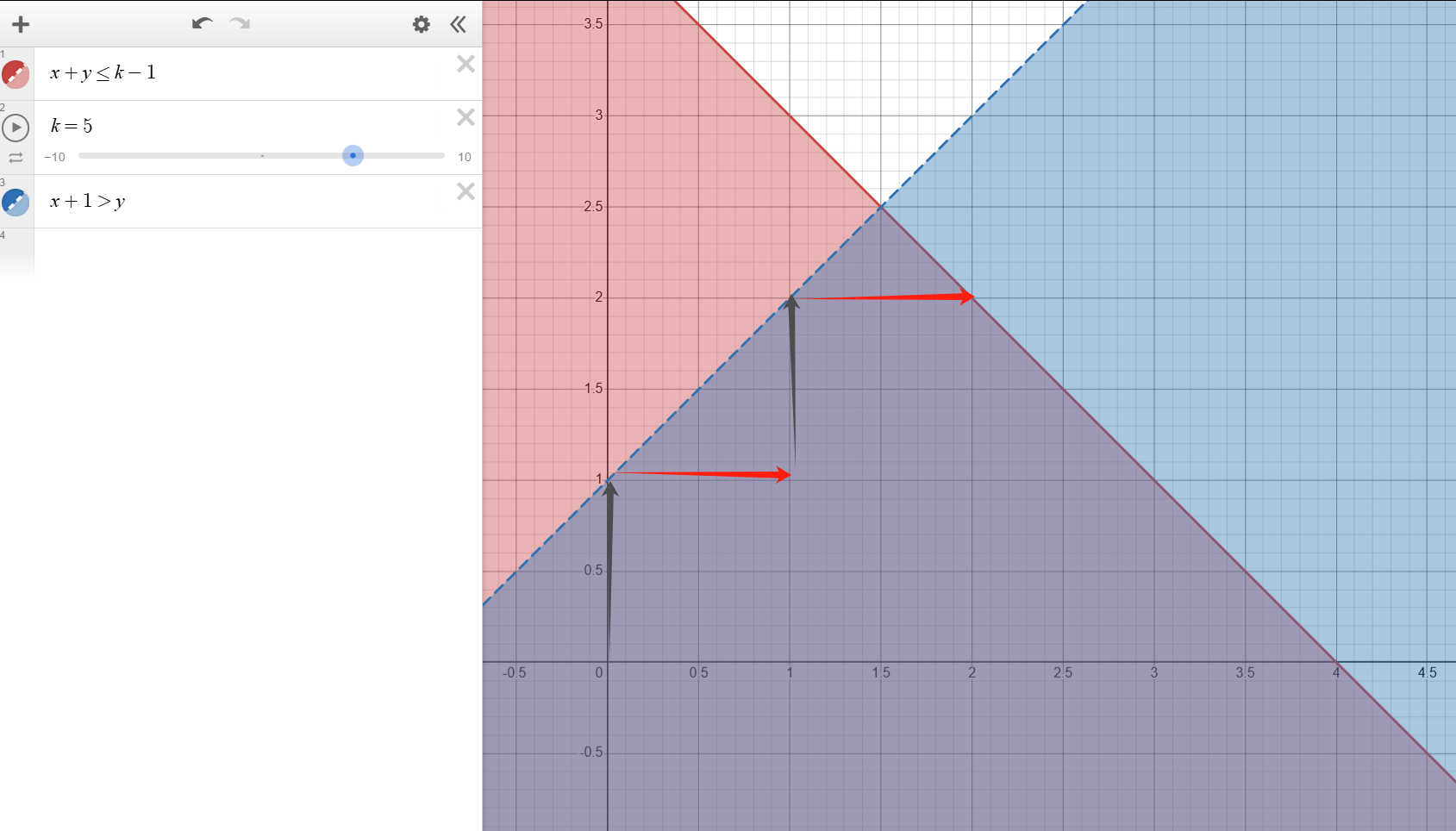
后半部分的做法完全相同。整个过程只需要枚举\(i=p+q\le k\),要提前预处理阶乘,总\(O(n+m)\)。
G
hh仙人构造题场上无人领悟出题人高妙而深刻的思想,而且题解有神秘bug我不知道出题人是怎么处理的,我乱搞了一下他过了但是我不会证明不过我还是写一下我咋过的,,
场上的思想成果是,想到勾股数自然想到神必经典通解\((2uv,u^2-v^2,u^2+v^2)\),然而并不知道有何吊用。但是我想到了怎么判无解hh,如果有\(S\),\(T\)里面有1或2就是无解,思想成果颇丰
外星智慧出题人一来就是神之一笔:注意到过程可逆我们只需要把一个数搞成4。接下来‘他又是一波妙笔频出:::
有抽象变换之\(8k,15k,12k,5k,4k\),,,,免费减少2的幂次好好呼哈
可以对当前的数字\(x\)维护\((p,q)\)满足\(x=2^cpq\),\(p,q\)都是奇数。初始第一次可强制\(q=1\)。。然后,我们用\(u^2-v^2=(u+v)(u-v)\to 2uv\)这个变,产生新的\((p',q')=maxmin(getaway2(\frac{p+q}2),getaway2(\frac{p-q}2))\),\(getaway2\)表示除去2的因子。为防爆\(1e18\)我们使用上方的妙笔及时消除2,,由此进行一个勾八迭代我们智慧的发现只需要迭代到\(p,q\)都变成1就行,然后迭代是log次(写不动了反正不难证明kjdfhliadsf,大概就是连着做两次发现\(p,q\)较大的那个至少减半,要小讨论)
上面的看起来非常美妙额,但是一写代码tmlgb就发现如果迭代到\(p=q\)就寄,我浅打补丁此时令\(p'=p^2,q'=1\)它水过,然而不明真相那我就当白嫖ac了哈哈哈哈哈哈哈哈
什么,,?吃个晚饭先
破案了我草,迭代的时候永远不会出现\(p=q\),因为显然一直满足\(\gcd(p,q)=1\)。之前写代码\(assert\)挂了是因为我放错地方了,出现\(p==q\)的时候一直是\(p=q=1\)。。。爆笑呵呵哈哈呼呼哈哈好
K
首先这题就很像分层图+最小割+网络流然后somehow搞一搞,实际上这题也确实是这样做的。
点上的限制不好做,拆点把限制放边上,然后建 \(k\) 层分层图,令 \((n,k,ty)\) 表示第 \(k\) 层的点 \(n\) 的入点/出点,建图为:
- 超级源点向源点 \((s,0,1)\) 连边,汇点 \((t,k-1,0)\) 向超级汇点连边,边流量 \(\infty\)。
- 原图中的每一条边 \(u,v\),连边 \((u,j,1)\to (v,j,0)\),流量 \(\infty\)。
- 每一层之间连边 \((i,j,0)\to(i,j+1,1)\),表示永远可以使用一次代价走到上一层,流量 \(\infty\).
- 每个点出点入点间连边 \((i,j,0)\to(i,j,1)\),流量为 \(1\),表示该边断开代价为 \(1\)。
然后这张图的最小割就是答案,跑一遍网络流即可,然后根据边流量输出方案,时间复杂度 \(O(nmk)\)。
然后众所周知一个网络流对应一个线性规划,这题能用线性规划优化到 \(O(nm\log n)\),做法如下:

