123
Day1
E
记录一下 \(\sum i^2p_i,\sum ip_i\) 和原串的哈希,注意到
\[ (\sum i^2p_i)' - \sum i^2p_i=(i-j)(i+j)(p_i-p_j)\\ (\sum ip_i)' - \sum ip_i = (i-j)(p_i-p_j) \]
所以for一遍再用哈希判断是否相等即可。
G
插头dp板子题,状态 \(f_{j,i,s_1,s_2,s_3,st}\) 表示当前插到了 \((i,j)\),放了 \(s_1/s_2/s_3\) 个1/2/3,边缘状态为 \(st\) 时的方案数,预处理方案与转移即可,方案数 \(<2400\),就能通过,详见代码。
1 | signed main() { |
H
怎么[deleted]还卡空间
补这个题才发现这个题牛客出过。题意是,问一个n个点的树删一些点能不能跟另一颗m个点的树同构,\(n\le 1e5,m\times n\le 1e7\)
把第一棵树看作有根,第二个树看作无根。考虑dp,\(f[u][a\to b]\)表示能不能第一个树上\(fa(u)\to u\)的边与第二颗树上的\(a\to b\)匹配,然后u下面子树跟第二棵树b那半边匹配。然后这个dp转移是枚举u的儿子,b除了a之外的出边做一个二分图匹配,能匹配满\(f[u][a\to b]\)就是1。这个dp状态是O(nm)的,然后匹配还有复杂度所以跑不了。
考虑优化。固定u和b,对b的所有邻居a一起求\(f[u][a\to b]\)。可以把u的所有儿子和b的所有邻居二分图匹配,假设b的邻居有cnt个。如果匹配结果是cnt,那么说明直接把u作为匹配的lca,找到了答案,直接回答YES。否则如果匹配结果小于等于cnt-2,说明所有\(f[u][a\to b]\)都是0。否则匹配结果等于cnt-1,把唯一没匹配的b的邻居找出来跑dfs增广一下,能增广到的点a说明\(f[u][a\to b]\)是1。这里相当于尝试撤销一个点a,把a往u的父亲上匹配。
考虑复杂度。要跑的匹配的总边数是\(\sum_{a\in T1,b\in T2}deg_{T_1}(a)\times deg_{T_2}(b)=O(nm)\)。匈牙利算法的复杂度有点容易想错:每个第二棵树上的m个点与第一棵树上的每一个点相当于只会出现于这些匹配中一次,总复杂度应该是\(O(\sum_{a\in T_1} deg(a)\times m\times\min(deg(a),m))\),把min放缩成m, 是\(O(nm^2)\)的,常数小且难卡所以能跑过。写dinic的话可以\(O(nm\sqrt m)\),这个就稳过了。
dp数组很容易爆空间,反正最后是开的bitset,但是bitset需要变长,所以手动写了一下bitset。
Day2
A
首先在第 \(i\) 次约会的女孩在前 \(i\) 次约会的女孩中的排名是均匀分布的,那么记 \(f(i,j)\) 表示第 \(i\) 次约会的女孩在前 \(i\) 个女孩中排名为 \(j\) 时的期望颜值,那么如果在第 \(i\) 次选,那么期望颜值为
\[ E = \frac{1}{i} \sum_{j=1}^i f(i,j) \]
令 \(ans[i]\) 表示从第 \(i\) 次开始计算时的期望答案,John会根据当前的女孩的颜值排名决定是否继续,那么转移为
\[ ans[i]=\frac{1}{i}\sum_{j=1}^i\max\{ans[i+1]-cost,f(i,j)\} \]
考虑如何计算 \(f(i,j)\),显然 \(f(n,i)\) 已知,那么往前推,每次考虑删掉的在前面还是后面,有
\[ f(i,j)=p\cdot f(i+1,j+1)+(1-p)\cdot f(i+1,j)\quad \text{where}\quad p=\frac{j}{i+1} \]
B
这两天有点摆,一直在吃喝玩乐,直到今天才有空写一写题。字节营打的还算能交差吧,然后回重庆规律作息了两三天,摸了摸猫猫,感觉现在精神状态得到了极大恢复。
题意是有至多50个点,每个点有各自的概率是红色或蓝色。问你红色点凸包和蓝色点凸包的交的面积的期望是多少。
这个题是没见过的套路,虽然这个套路挺简单的应该能场上yy出来。。。果然几何题就没有难题,就是比普通题写着折磨一些。考虑两个凸包\(P_1,P_2,...,P_n\)和\(Q_1,Q_2,...,Q_n\)的公共面积怎么算。除了暴力大力半平面交,还可以利用集合交运算的分配律。公共面积可以表示为
\[ \sum_{i=1}^n\sum_{j=1}^m S(triangle(O,P_i,P_{i\ mod\ n+1})\cap triangle(O,P_i,P_{i\ mod\ n+1})) \] \(triangle(\cdot,\cdot,\cdot)\)表示三个点形成的有向三角形,\(S(\cdot)\)是面积。两个有向三角形求交的面积,其值表示对应的正三角形求交后的面积,然后面积的符号是两个三角形方向的乘积。
如果能这样拆贡献,后面的做法就跟2024牛客第10场C的做法一样了。\(O(n^4)\)枚举两个凸包上的两条线段,然后再\(O(n)\)枚举其余的所有点,根据相对于两个凸包的位置乘上\(1,p[i],1-p[i]\)或\(0\)就行了。总共\(O(n^5)\)。两个三角形求面积交的函数有点难写,虽然也可以直接写个半平面交就是了,但是这样跟写一堆if也差不多麻烦。
D
原图是一个基环树森林,先考虑一个基环树,设环长为 \(c\),大小为 \(s\),那么走了 \(s+c+t\) 步的效果和 \(s+t\) 步的效果是一样的,就可以把概率多项式降幂到 \(s+c\),具体地不断重复 \(P_x\to P_{x-c}\) 后丢弃 \(P_x\) 即可。同时我们发现一个基环树在降幂过程中的行为只和 \(c\) 有关与 \(s\) 无关,这启示我们一起处理环长相同的基环树,那么不同的组数只有 \(O(\sqrt{n})\) 种,降幂操作的总复杂度就为 \(O(m\sqrt{n})\)。
对于环长为 \(c\) 的一组基环树首先可以计算概率多项式 \(P(x)=\sum_{i=0}^{c+s-1}p_ix^i\),其中 \(s\) 取该组中最大的树大小,在计算 \(P^k(x)\) 的过程中保持幂次为 \(c+s-1\),那么单组复杂度就为 \(O(s\log s\log k)\),总复杂度为 \(O(n\log n\log k)\)。注意我们可以通过大树的概率多项式降幂得出小树的概率多项式。
考虑如何计算答案,为便于处理,在基环树的环上选取一个点 \(x\) 作为根,将 \(x\to a_x\) 这条边视为额外边,先统计经过额外边的路径贡献。显然若 \(C(x)=\sum_{i=0}^sc_{s-i}x^i\) 其中 \(c_{s-i}\) 表示深度为 \(i\) 的点的个数,那么 \([x^{s+d}]C(x)\cdot P(x)\) 就为经过额外边后又多走了 \(d\) 步的贡献,直接线性累加即可。总复杂度为 \(O(n\log n)\)。
考虑如何计算不经过额外边的路径贡献,对于一个点 \(u\),令 \(c'_i\) 表示以 \(u\) 为根的子树中深度为 \(i\) 的点数量,那么这个点的答案就是 \(\sum p_ic_i\)。为了加速这一过程,注意到一个点的贡献来源只能是子树内,那么跑dfs序,一个点的贡献来源就是一段区间。考虑对区间分块,块大小 \(B\),对于每段区间分别计算 \(C_i(x)\) ,其定义与 \(C(x)\) 一样,但是只统计该区间内的点,将其与 \(P(x)\) 相乘,那么对于一段完整的区间就可以 \(O(s\log s)-O(1)\) 得到答案,剩下的点数为 \(O(B)\),那么总复杂度即为 \(O(\frac{s}{B}s\log s+sB)\geq O(s\sqrt{s\log s})\),当 \(B=\Theta(\sqrt{s\log s})\) 时取到最小值。总复杂度为 \(O(n\sqrt{n\log n})\),操作上可以取 \(B=2000,4000\) 等。
E
[deleted]
题意是,有一个多边形,然后有一个弹性绳子。这个绳子只能在多边形外部和边界上,并且会跟多边形绝对光滑无摩擦力地收缩。给出了绳子的起点和终点,问你这个绳子的最长长度是多少。你可以决定这个绳子的绕法,绳子严格不允许任何位置自交。放个图,图示了两种绕法。

这个题需要有一个神奇观察。就是,如果这个题要让绳子只能在多边形的内部和边界上,那就是直接建图(如果一条对角线完全在多边形内部或边界上就连边)跑最短路就行。因为绳子会依照最短路的走法收缩成对应的形态。后面的推导需要这个观察。
然后,针对原来这个多边形,如果我们求一个凸包,那么相邻的凸包顶点之间会形成一些洞。
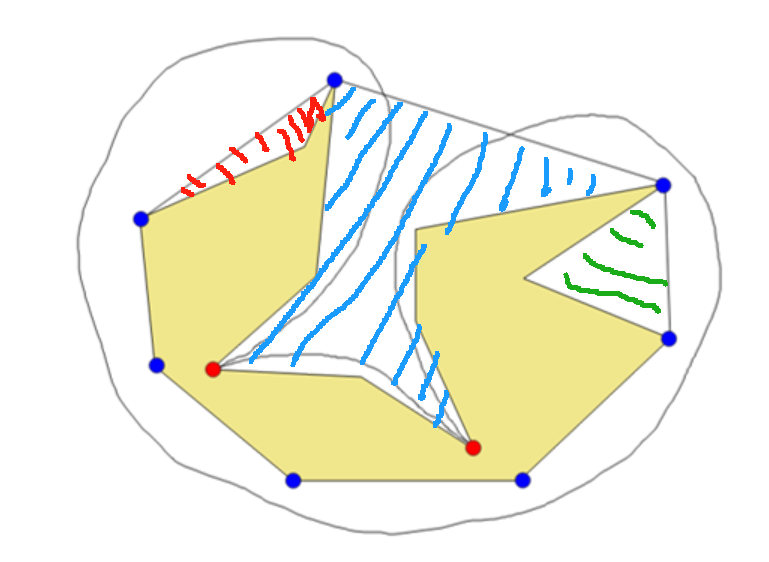
然后针对这些洞,我们发现洞内(比如说,上面的蓝色区域内)形成一个多边形,洞内如果有弹性绳子,绳子就会走最短路(根据上面的观察)。如果一个洞内的点要连一条绳子到洞外面,那弹性绳子肯定首先会走最短路到达洞的端点,然后再凸包上面再走。
那么,如果起始点不在同一个洞里面,绳子的绕法一定是
第一段,起点到洞端点
第二段,洞端点到洞端点(凸包上连续的一段)
第三段,洞端点到终点
如果在同一个洞里面,有两种绕法
直接洞内连接,走最短路
到洞端点,绕一圈,再进洞
这种case需要讨论是否合法,因为进洞出洞有可能凸包会跟自身重合,如下图

这些情况跑最短路就可以了,判同一个洞里的情况还需要跑最短路的时候记录一下上一条边,方便check。
这中间有一个比较难的小点,是建图判断一条对角线是否不经过多边形内部。最后的写法是,对角线顶点必须满足辐角范围,然后其他线段都跟对角线严格不交(没有公共点)。因为,如果一条对角线在中间蹭过了多边形边界,虽然他也可行,但是它可以被分割成多条不蹭过多边形的对角线,然后被等效替代。而且,判断这种蹭过的合法性很难,到时候判断路径有没有交点也有一些问题。因此就避开。除此之外,把多边形的边加入图中,这个图就算完全ok了。
呵呵在然而,判断两条线段是否严格不交也有赤石细节,,,主要是得特判线段共直线。粘下代码。
1 | int segcross(int a, int b, int c, int d) { // do seg ab and cd have any common point? yes 1, no 0. |
补这个题比便秘还难受。pengbo补这个题+35,然后prismatic encore他们过了的题解还被我hack了,曲曲折折。[deleted]
G
可持久化可并堆板题,已经加板子里了。
H
枚举钦定一端点为 \(x\),考虑另一端点 \(y\) 需要满足的条件,将 \(x\to y\) 路径上的点0-index重标号为 \(0,1,\dots,S\),且对路径上每个点 \(i\) 处理出从 \(i\) 开始不接近路径的最长路长度 \(v\),考虑路径上面的两点 \(p_1<p_2\),最长路为 \(v_1,v_2\),那么需要满足
- \(p_2-p_1+v_1+v_2\leq X\) 且
- \((S-1)-p_2+p_1+v_1+v_2\leq X\)
对于第一个条件满足的点对显然不用处理,对于第一个条件不满足的点对,相当于在每个 \(p_2\) 上有一个向下最长伸长 \(lim\) 个节点的限制,\(lim\) 值即为 \(\min X-((S-1)-p_2+p_1+v_1+v_2)\),就是
- \(p_2-p_1+v_1+v_2 > x \Longleftrightarrow v_1-p_1 > X-p_2-v_2\)
- \(\min X-((S-1)-p_2+p_1+v_1+v_2) \Longleftrightarrow \max v_1+p_1\)
对于一个点及其 \((v,p)\),转化为 \((v-p,v+p)\) 后就是一个动态RMQ问题,可以用主席树维护,在dfs过程中动态加入 \((v,p)\),在末尾判断是否满足条件即可统计答案。
本题需要计算子树内的最长路径,子树内最长路径超过 \(X\) 的同样不满足条件。
I
表示大小关系有一个很自然的相反是建图连边,注意到 \(\sum k_i\leq 2\times 10^5\),可以线段树优化建图,后面的问题是一个裸的差分约束问题,但是观察题目性质,发现图中存在环则无解,所以可以不用跑spfa,直接dfs判环后跑拓扑排序即可。
K
首先差分,求 \(f(r)-f(l-1)\),即求 \(f(X),X\leq N=8\cdot 10^{16}\)。
观察1: 对 \(ab^c\) 计数等价于对 \(ab^2,ab^3\) 计数。也即
\(\#\{ab^c|a<b,b>1,c>1,ab^c\leq X\}=\#\{ab^2|\dotsb\}\cup\{ab^3|\dotsb\}\)。
- 对于 \(k>1\)
- \(ab^{2k}=a(b^k)^2\),所以这种情况是 \(ab^2\)
- \(ab^{2k+1}=(ab)\cdot(b^k)^2\),由于 \(a<1,k>1\) 故 \(ab\leq b^2\leq b^k\),故这种情况也是 \(ab^2\)
- 综上,只需对 \(ab^2,ab^3\) 计数
考虑计算 \(\#S_2=\{ab^2|a<b,b>1,ab^2\leq X\}\)
- 对于每一个整数 \(n\) 都有二次唯一划分 \(n=ab^2\) 使得 \(a\) 无平方因子
- 注意到 \(n\in S_2\) 等价于 \(n\) 的二次唯一划分满足 \(a<b\)
- \(n\) 的二次唯一划分满足 \(a<b\) 推 \(n\in S_2\) 显然
- 由 \(n\in S_2\),设 \(n=a'b'^2,a'<b'\),那么 \(n\) 的二次唯一划分 \(n=ab^2\) 满足 \(a\leq a'<b'\leq b\),故 \(n\) 的二次唯一划分满足 \(a<b\)
- 于是可以枚举无平方因子的 \(a\),考虑 \(b\in[a+1,\sqrt{X/a}]\),由上述等价关系,实际上所有在该范围内的 \(b\) 唯一对应一个 \(n\in S_2\)
- 考虑枚举复杂度,\(a<b,ab^2\leq X\) 故 \(a\leq \sqrt[3]{X}\),实际上 \(a\) 只有大约 380,000 个。
考虑计算 \(\#S_3=\{ab^3|a<b,b>1,ab^3\leq X\}\)
- 定义 \(n\) 的三次唯一划分为 \(n=xy^3\) 且 \(x\) 无三次方因子,类似于 \(S_2\) 的处理可得。
但是简单相加显然会算重,考虑如何去重。
暴力做法是枚举 \(S_3\) 中元素,但是在 \(N\) 范围内 \(\#S_3>2\cdot 10^8\),不可行。
考虑集合 \(S_3-S_2\),考虑 \(n=xy^3=ab^2,a\geq b,n\in S_3- S_2\),此时若 \(\exist p|(a,b)\),我们发现 \(m=x(y/p)^3=(a/p)\cdot(b/p)^2\) 同样满足 \(a/p\geq b/p,m\in S_3- S_2\),同时我们还发现该操作可逆,可以同时乘上一个 \(p\) 产生新的 \(S_3- S_2\) 中元素。
这启发我们可以把 \(S_3- S_2\) 划分为若干个等价类,每个等价类中有一个源 \(S=xy^3=ab^2,(a,b)=1,a\geq b\),且该等价类中的数都能由源产生。考察源的性质
- \((a,b)=1\Longrightarrow (a,y)=1\)
- 若 \((a,y)=t\neq 1\),那么 \(S=x(ty')^3=ta'b^2\),那么必然有 \(t|b\),矛盾,故 \((a,y)=1\)
- 于是可以设 \(x=x_2a\),有 \(S=x_2y^3=b^2\),同时 \((a,b)=1\Longrightarrow (a,x_2)=1\)
- 若 \((a,x_2)=t\neq 1\),则 \(t^2|x=ax_2\),那么 \(t|b,(a,b)\geq t\),矛盾,故 \((a,x_2)=1\)
- 考虑限制 \(a\geq b\),等价于 \(a\geq \sqrt{x_2\cdot y^3}\),令 \(k=\sqrt{x_2\cdot y}\),等价于 \(x=a\cdot x_2\geq x_2\cdot y\sqrt{x_2\cdot y}=k^3\)
- 考察有效源的数量,有 \(k^3\leq x,xy^3\leq X,x<y\),于是 \(x\leq \sqrt[4]{X},k\leq \sqrt[12]{X},xk\leq \sqrt[3]{X}\approx 430,000\)
考虑如何枚举源
- 固定无三次方因子的 \(x\),对于 \(k^3\leq x\),令 \(y=k^2/(k^2,x),a=x/(k^2,x)\),那么有 \(ak^2=xy\),于是 \(S=xy^3=a(ky)^2\)
- 由于 \(S\) 唯一对应一组 \((x,y,a,b,k)\),且合法的 \(S\) 必然有无平方因子的 \(a\),那么只需考虑无平方因子的 \(a\) 即可生成所有源
考虑如何计算 \(\#S_3-S_2\)
- 对于一个源 \(S\),它所生成的数形式为 \((aP)(bP)^2\),只要 \(P\) 无平方因子且与 \(a\) 互质,该数就在这一等价类中
- 考虑 \(n=x(yP)^3,x<yP\),于是 \(P>x/y\),又 \(x(yP)^3\leq N\),于是 \(P\leq \sqrt[3]{N/x}/y\leq \sqrt[3]{N}\)
- 故剩下的问题是计算 \(F(n,a)\) 表示 \(\leq n\) 的数中无平方因子且与 \(a\) 互质的数个数,范围在 \(a,n\leq \sqrt[3]{N}\leq 500,000\) 中
计算 \(F(n,a)\)
- 显然 \(F(n,1)\) 由筛法易得。
- 考虑 \(F(n,2)\),由容斥原理,\(F(n,2)=F(n,1)-U(n,2)\),其中 \(U(n,d)\) 表示 \(\leq n\) 中是 \(d\) 的倍数的无平方因子数个数。
- \(F(n,6)=F(n,1)-U(n,2)-U(n,3)+U(n,6)\)
- \(F(n,\prod_i p_i)=\sum_{S}(-1)^{|S|}U(n,\prod_{i\in S}p_i)\)
- 由于500,000中的数最多只有6个不同质因子,故可以直接暴力做
该算法的复杂度大约为 \(O(2^{\omega(\sqrt[3]{n})}\sqrt[3]{n})\),其中 \(\omega(n)\) 为 \(\leq n\) 中不同质因子的最大个数。
主要代码:
1 | vector<vector<int>> U(M + 1); |
Day3
E
不知道我补这么个水题为啥这么痛苦
这个题关键是求一个点辐射出的一个固定形状的凸包内部的点的权值和。可以把凸包拆分成很多梯形,然后梯形数点可以变换坐标求:要数\(y=kx+b\)下方的点,令\(y'=y-kx\),梯形就变成了矩形。
这个题让我把double的精度问题彻底想明白了。
首先,float是6-7位有效数字,double是15-16位有效数字,long double是18-19位有效数字。具体用起来很难把握,尽可能避免用浮点比大小。
这个题,梯形数点的时候涉及到了一些小边界情况:如果是梯形的上边缘,点要取等,防止少算上边界;如果是下边缘,点不取等,防止多减去下边界。因此,对变换后的\(y'\),由于边界问题,如果double存\(y'\),数点会有精度误差。有一些简单的解决办法:可以对\(y'\)离散化,把\(y\sim y+eps\)范围内的都离散化成一个点;可以考虑把所有上边界都\(+eps\),把下边界都\(-eps\),然后无脑跑就完了;也可以把询问和点塞结构体里面,然后比较的时候如果差小于\(eps\)视为相等,再比较请求类型。这些做法都可以,问题是这个eps怎么取。
这个题向量坐标\(1e3\),因此凸包坐标\(1e4\),因此\(y'=y-kx\)里面的斜率\(k\),如果不是0,绝对值最小是\(1e-4\),最大是\(1e4\)。然后原坐标\(x,y\)(包括算上凸包扩散,因为凸包坐标\(1e4\),时间\(1e5\),扩散坐标\(1e9\),原坐标\(1e9\))范围是\(1e9\)。因此变换后的\(y'\)是\(1e13\)。结合一下,因此\(y'\)的精度要求为,量级\(1e13\)的情况下需要保持\(1e-4\)的绝对误差,总共17位有效数字。因此double是包过不了了。long double有18-19位,因此eps开到\(1e-5\)或\(1e-6\),就稳过。实际上这个题因为量级卡不满,开\(1e-7\)也能过。但是无脑上\(1e-9\)肯定long double也吃不住了。
不过最保险的做法还是,用分数表示,比较的时候用int128乘法比大小。如果要离散化塞vector就正常做,如果就直接排序的话,cmp把关系写清楚。下边界先来,然后是点,然后是上边界。
用浮点排序确实省事了,但是精度问题必须得算清楚,不然似的不明不白。。

F
考虑固定一个根及答案 \(x\) 的时候怎么做,显然加边的一个端点必须为根,否则不优,之后有个贪心,每次选择深度最深的点,往上跳 \(x-1\) 步祖先,后根向祖先连边,选择 \(k\) 次之后判断一下是否满足条件即可,这样做看上去就很对。
然后考虑如何加速这个过程,找最深的点其实就是离根距离最大的点,那么可以维护一个线段树,支持取max和区间加,每次选出来一个点后就将部分点排除,排除的时候可以用dfn序,把排除的点变为一个连续的区间,这样就可以维护了,单次check复杂度为 \(O(k\log n)\)。
注意到答案显然是有单调性的,可以二分答案,那么对于一个根复杂度就是 \(O(k\log^2n)\)。
考虑如何做整个,实际上我们需要的信息只有深度,而深度在移动根的时候是可以简单维护的,那么每次换根的时候在线段树上用dfn序维护一下深度即可,维护深度总复杂度为 \(O(n\log n)\)。
再注意到相邻两个点的答案相差不会很大,实际上最多相差1,于是我们可以在换根的过程中把二分的 \(\log\) 砍了,总复杂度为 \(O(nk\log n)\)
G
考虑 \(k=O(\log n)\) 怎么做,可以把 \(0\sim n-1\) 按照线段树划分,当Anna走到某个房间 \(i\) 时,填入最浅的只剩 \(i\) 没有访问过的那一层的深度 \(-1\),如已经访问了 \(\{0,1,3\}\),现在访问了 \(2\),那么那一层就是表示区间 \([0,3]\) 的那一个线段树节点。
Bertil查询时对当前区间的1的数量分类讨论
- 如果只有1个1,那么说明那个房间在区间另一半,可以递归下去
- 如果有2个1,那么答案必然是两个1的其中1个
考虑如何做到 \(O(\log \log n)\),将前 \(n-O(\log n)\) 个数都涂成 \(k\) ,最后留下 \(O(\log n)\) 个数跑上面的做法。
- 如果最后Emma填的数不为 \(k\) ,那么可以解决
- 如果最后Emma填的数为 \(k\) ,Anna可以额外记录一下最后 \(O(\log n)\) 个数的和模 \(n\) 的值,并将其encode到序列中,这样Bertil就能求和后作差得到答案
具体实现上取 \(O(\log n)=32\),将 \(sum\) 对 \(n/2\) 取模,然后把 \(sum\) encode到16个必然出现的5上,对应二进制位为1则将5变为6,这样就能唯二确定答案位置。
H
补个小清新题清新口气。这个题还是有点小细节的,但还好。
从某个下标分界点开始,前半部分是把序列按值域强行划分为上下两半,后面是一个从某个值域分界点开始的向上的LIS和向下LDS。
考虑枚举这个下标分界点前的最后一个位置\(i\),假设\(a[i]\)属于下半部分。那么\(a[1,...,i]\)中,\(\le a[i]\)的都划分给递增序列,\(>a[i]\)都划分给递减序列。令\(f[i]\)表示把\(a[1,...,i]\)中\(\le a[i]\)的挑出来,前缀最大值的位置有多少个。\(g[i]\)表示把\(a[1,...,i]\)中\(\ge a[i]\)的挑出来,前缀最小值的位置有多少个。这俩都很好转移。令\(LIS(i,x)\)表示\(a[i,...,n]\)的第一个位置\(\ge x\)的LIS长度是多少,令\(LDS(i,x)\)表示\(a[i,...,n]\)的第一个位置\(<x\)的LDS长度是多少。当\(a[i]\)属于下半部分,则\(Ans\)对\(\max_{i\le j\le r}\{f[i]+g[r]+LIS(i+1,j)+LDS(i+1,j)\}\)做个checkmax,其中\(r=argmin_{r< i,a[r]>a[i]}\{a[r]\}\)。类似,当\(a[i]\)属于上半部分,则\(Ans\)对\(\max_{l\le j\le i}\{f[l]+g[i]+LIS(i+1,j)+LDS(i+1,j)\}\)做个checkmax,其中\(l=argmax_{l< i,a[l]<a[i]}\{a[l]\}\)。然后因为实际上\(f[i]=f[l]+1,g[i]=g[r]+1\),所以只需要\(Ans\)对\(f[i]+g[i]-1+\max_{l\le j\le r}\{LIS(i+1,j)+LDS(i+1,j)\}\)做checkmax。
然后这个题需要提前dp一遍LIS和LDS,把那些区间加的操作取出来,方便正着枚举\(i\)的时候回退。
Day4
E
注意到最终串形如aaabbbccc...再加上一个后缀,那么可以 \(O(26\log n)\) 二分求出该串,最后二分哈希判断一下大小即可。
J
对于一个 \(i\),若其最终向左倒,那么其右边的东西是不重要的。同时注意到一个单调性,对于一个 \(i\),要使 \(i\) 向左倒,左边界越远越不劣,存在一个界 \(a_i\leq i\),使得对于 \(\forall l\leq a_i\),\(i\) 都能向左,向右倒同理有 \(b_i\geq i\)。
考虑如何求这 \(a_i,b_i\),\(b_i\) 与 \(a_i\) 对称,故只求 \(a_i\)。由于存在单调性,于是可以做整体二分,每次维护 \([L,R)\),以及一个id的集合 \(S\),表示在 \(\forall i\in S,a_i\in [L,R)\),然后二分中点 \(M=\frac{L+R}{2}\),从 \(M\) 开始向右扫,在扫的过程中维护一个栈,表示还没有倒下的id,每次加入一个 \(i\) 的时候先弹栈,后判断 \(i\) 能否向左倒,若能则将 \(i\) 归入 \(A\),否则将 \(i\) 归入 \(B\),然后就可以递归下去。
1 | auto dfs = [&](auto self, int L, int R, vector<int> ve) { |
考虑求出了 \(a_i,b_i\) 如何计算答案,实际上需要计算 \((l\leq a_i\land i\leq r)\lor(l\leq i\land b_i\leq r)\) 的 \(i\) 个数,容斥一下,表示成
\[+\#l\leq a_i\land i\leq r\] \[+\#l\leq i\land b_i\leq r\] \[-\#l\leq a_i\land i\leq r\land l\leq i\land b_i\leq r=\#l\leq a_i\land b_i\leq r\]
然后就是一个二维偏序,扫描线+树状数组即可。
Day5
D
如果询问的是划分个数,那么可以直接 \(f_{i,j,t}\) 表示区域 \([i,i+2^t)\times[j,j+2^{t+1})\) 区域内的合法划分个数。
考虑如何做不同方案,可以容斥。每次转移的时候 \(2^5\) 枚举一下同时满足的划分方案,然后就能把 \(2\times 4\) 矩形分为若干 \(1\times1,1\times2,2\times1\) 的小方块,然后引用容斥原理即可。
具体实现上记 \(f_{i,j,t}\) 为 \([i,i+2^t)\times[j,j+2^{t+1})\) 上的合法方案数, \(g_{i,j,t}\) 为 \([i,i+2^{t+1})\times[j,j+2^t)\) 上的合法方案数, \(h_{i,j,t}\) 为 \([i,i+2^t)\times[j,j+2^t)\) 上的合法方案数,那么转移可以写出。可以写一个小程序生成转移。
1 | vector<vector<vector<u64>>> ve; |
F
首先是一个神秘转化 \(b+i|a+wi^2\Longleftrightarrow b+i|a+wi^2+w(b-i)(b+i)=a+wb^2\)。那么 \(f(a,b)=k\) 即为 \(lcm(b,b+1,b\dots,b+k)|a+wb^2\),对原式做差分,即求
\[ \sum_{k=1}^\infty\sum_{a=1}^A\sum_{b=1}^B\left[ lcm(b,b+1,\dots,b+k)|a+wb^2 \right] \]
固定 \(b,k\),符合条件的 \(a\) 的数量为
\[ \left\lfloor \frac{A+wb^2}{lcm(b,b+1,\dots,b+k)} \right\rfloor- \left\lfloor \frac{wb^2}{lcm(b,b+1,\dots,b+k)} \right\rfloor \]
则答案为
\[ \sum_{b=1}^B\sum_{k=1}^\infty \left\lfloor \frac{A+wb^2}{lcm(b,b+1,\dots,b+k)} \right\rfloor- \left\lfloor \frac{wb^2}{lcm(b,b+1,\dots,b+k)} \right\rfloor \]
当 \(k\geq 2\) 时,\(lcm(b,b+1,\dots,b+k)\geq b(b+1)(b+2)\geq\frac{b^3}{2}\),故当 \(b\geq 2(w+\sqrt[3]{A})\) 时值为 \(0\),故直接枚举 \(b,k\) 即可求出这部分贡献,枚举 \(k\) 复杂度显然很低,复杂度 \(O(w+\sqrt[3]{A})\)。
当 \(k=1\) 时,\(lcm(b,b+1)=b(b+1)\),则原式为
\[ \sum_{b=1}^B \left\lfloor \frac{A+wb^2}{b(b+1)} \right\rfloor- \left\lfloor \frac{wb^2}{b(b+1)} \right\rfloor =\sum_{b=1}^B \left\lfloor \frac{A-wb}{b(b+1)} \right\rfloor- \left\lfloor \frac{-wb}{b(b+1)} \right\rfloor \]
对于 \(\sum\limits_{b=1}^B\left\lfloor\frac{-wb}{b(b+1)}\right\rfloor=\sum\limits_{b=1}^B\left\lfloor\frac{-w}{b+1}\right\rfloor\) 可以直接枚举 \(b\) 求和,复杂度 \(O(w)\)。
对于 \(\sum\limits_{b=1}^B\left\lfloor\frac{A-wb}{b(b+1)}\right\rfloor\)
- 当 \(b\leq 2(w+\sqrt[3]{A})\) 时,暴力枚举
- 当 \(b>\frac{A}{w}\) 时,\(\left\lfloor\frac{A-wb}{b(b+1)}\right\rfloor=-1\),可以直接求出
- 此外,注意到 \(b\geq\sqrt[3]{A}\),故 \(\left\lfloor\frac{A-wb}{b(b+1)}\right\rfloor\leq\sqrt[3]{A}\),故可枚举值域,每次二分求出值对应的 \(b\) 的区间即可求出答案。
该部分复杂度 \(O(\sqrt[3]{A}\log \frac{A}{w})\)。
1 | void solve() { |
J
首先考虑最小时间,毛估估一下就感觉必须要 \(1\sim n\) 个人依次进入,依次转身,然后再走到座位,最小时间显然是 \((l+r)(n+1)\),而且这个下界是显然可以得到的。
考虑方案数,第一排的人显然不能跨过其他人,否则就会影响下一轮的启动,那么第一排的方案数就是 \(\binom{l+r}{l}\)。考虑其余排,最后一个人显然也不能被卡,有 2 种选座方案,倒数第 \(i\geq 2\) 个人不能影响最终的结束,于是只能选距离过道至多 \((n+1)(i-1)\) 远的位置,那么能选的座位数就是 \(\min\{l,(n+1)(i-1)\}+\min\{r,(n+1)(i-1)\}-(i-1)\)。排间是独立的,于是求出一排的方案快速幂起来就好。
1 | ll ans = C(l + r, l), t = 2; |