我再也不网络口嗨了
把之前的零碎撤下来整理了一下,再加上又做的一些新的,现在弄个总集篇传上来
现在做到024,赛季开始前再看一遍,要是能出线就这个赛季完了继续做
比赛链接 https://atcoder.jp/contests/agcXXX 把xxx换成编号
agc001
a
排序后贪心
b
类似gcd递归求解一个平行四边形的答案
c
枚举最后树的直径的中点/边
d
把每个位置视为点,相等关系视为边,一个偶数回文串会提供L/2个相等关系,奇数会提供\((L-1)/2\)个相等关系,最中间的位置没有信息。我们需要a和b提供的所有边让整个图联通,那么显然最后只有可能是环或链。如果A中有大于两个奇数显然无解。因为已经损失了三条边了,不可能构成环和链了。如果A中有两个以下奇数,就放在a的最开头和最结尾,以便构成链。然后不难构造:\(b[1]=a[1]+1,b[2\ldots m-1]=a[2\ldots m-1],b[m]=a[m]-1\)
e
答案是\(\sum_{i<j}\binom{a_i+a_j+b_i+b_j}{a_i+a_j}\)
考虑几何意义,即从\((0,0)\)走到\((a[i]+a[j],b[i]+b[j])\)方案数。平移,答案即对任意i和j,从\((-a[i],-b[i])\)到\((a[j],b[j])\)方案和。
考虑dp。把\(dp[-a[i]][-b[i]]\)初值\(++\),然后\(dp[i][j]+=dp[i-1][j]+dp[i-1][j]\)。这相当于利用组合递推的可加性,把n个起点的dp叠加起来一起做。
考虑\(i<j\)以及\(i!=j\),答案就是\(\frac{\sum_{i}dp[a_i][b_i]-\sum_{i}\binom{2(a_i+b_i)}{2a_i}}{2}\)
f
agc002
B
每个盒子维护一个\(tag[i]=0/1\)表示i中的球有可能是红球。然后移球的时候就传染。某个盒子移光的时候把tag改成0。初始\(tag[i]=(i==1)\)
C
求使\(a[i]+a[i+1]\)最大的i最后剪短就行。如果最大的\(a[i]+a[i+1]<k\)无解
D
克鲁斯卡尔重构树
E
SG,但需要画图观察。
F
又是我最不擅长的计数
age003
好沙比啊,才到D就切不动了
A
s和n不能只有一个,w和e不能只有一个
B
\(sigma(ceil(每个以0分割的连续段的和/2))\)
C
2操作相当于对同奇偶位置冒泡。答案是偶数位上的奇排名数
D
两个互斥集合选较大的那一个,全局至多一个立方数。
不过分解质因数不能完全分解。抄一个别人写的
由于 \(v≤10^{10}\),直接质因数分解显然是不行的。考虑如果一个质因子 \(p>\sqrt[3]{v}\),那么他最多只有 \(2\) 次。考虑先把$ p≤v$ 的质数全筛出来,剩下的那个数只可能是\(1,p,p2,pq(p,q∈Prime)\) 中的一种。\(1\) 不需要考虑,如果是 \(p^2\) 应该映射到 \(p\),\(p\) 和 \(pq\) 都应映射到他们的平方,所以只需要判断这个数是不是完全平方数就可以了。注意在映射的过程中,一旦超过 $10^{10} $立即停止就行了。
E
首先把\(q\)弄成单增的,新的\(q[]\)长为\(Q'\)。然后倒着模拟。
从最大的\(q\)倒着往前考虑,同时对每个位置维护一些形如\((a,b)\)的标记,表示把此时的序列无限循环,前\(1-a\)的位置每个数都被用了\(b\)次。初始的时候在最大的\(q\)那里放一个\((len[Q'],1)\),表示最后的序列每个数用了一次。然后模拟的时候把这个标记往前扔。不需要每个中间时刻都有所有标记,扔标记是可以跳过一些时刻的。取模后尽量往前扔就行了。每个标记扔一次少一半,最多扔\(\log\)次。扔标记的时候有一个二分,总共两个\(\log\)。拿vector存一下就行了
我说的太意识流了,但这就是我看到有篇题解说倒着维护之后的第一想法。也放一篇别人的题解
F
这后面的DEF是真难受啊,每道题都能想到最开始的前一半,但是后面就疲软了
其实感觉这几道题都没什么难的,但是怎么就是不会呢(菜鸡落泪)
不想写了 题解
agc004
建议改为
ABCD 200
EF 2000
B
枚举用了多少次咒语,每个颜色就是在一段里取个最小的
C
交错梳子
D
\(a[1]\)肯定等于1,然后剩下的是树。贪心。从最深的叶子往上,每k-1个改成指向1
一定要看清题啊,题目保证1在最开始的环上
E
没图没法看。直接放题解。
F
我会做树就不错了
agc005
A
栈倒序模拟
B
两边单调栈
C
找直径,剩下的点挂直径上
D
我竟切了900计数/jk 要知道但凡是个计数,再水我都能跪的
考虑容斥,发现不好枚举非法。因为如果\(a[ck]\)和\(a[(c+2)k]\)都非法,他们不能都是\((c+1)k\)。枚举非法的时候要排除这种两个指向同一个的情况。那就把\(1-n\)按照\(mod k\)分成k个类,每个类做个dp,算一下从第i个类中选定$1[n/k] $(或\(1\ldots [n/k]-1\))个位置让他们不合法,有多少种方案。然后所有的类合并的时候就像生成函数那样
E
做过,但众所周知切不切和做没做过相互独立
如果先手能到一条边,这条边的端点在后手的树上距离超过2,先手就可以无线横跳。否则先手只能到一个比较偏僻的点等死。
注意到先手能到\(x \iff disa(x,s)<disb(x,t)\).以这个为限制条件从s开始在a树上dfs。如果能dfs到某个能反复横跳的地方,-1。否则找一个\(disb(x,t)\)最大的地方等死。
F
我切了个1900?感觉只有900。
看到模数,察觉到异样。百度一下,发现是ntt模数。然后推狮子
\(Ans_k=\sum_{u}(^n_k)-(\sum_{fa[v]==u}(^{size[v]}_{\ \ \ \ k}))-(^{n-size[u]}_{\ \ \ \ \ \ \ k})\)
打开
\(Ans_k=n(^n_k)-\sum_{u!=root}(^{size[u]}_{\ \ \ \ k})+(^{n-size[u]}_{\ \ \ \ \ \ \ k})\)
后面是个以size为下标的差卷积。
agc006
C
期望有线性性。递推的时候直接拿期望推期望。
这题的突破口在于,坐标x关于坐标y或z对称,等价于关于(y+z)/2对称。那么如果我们维护a[i]的差分,a[i]关于a[i-1]和a[i+1]对称等价于交换i与i-1之间的距离和i+1与i之间的距离。然后把转置拿出来,然后快速幂。
D
你妈,又是d题就干不动了,真tm菜
首先,二分答案。原题转化成01序列,求答案。手推一下,距离中间位置最近的连续两个相同的就是答案。
e.g,\(n=5,0010[1]0110\),方括号是中间位置,那两个连续的1比那两个连续的0距离中间位置更近,所以答案就是1
E
没看题解,但是自己没调出来去看了下数据,所以勉强算是自己切的把/jk
每一列用\(±b[i]\)表示这是第几列,是正序(+)还是逆序(-)。然后他连续三个交换的操作其实就是分别对奇位置和偶位置排序。
观察,发现有以下性质:偶位置的总翻转次数的奇偶性与奇位置的逆序对数奇偶性相同,反之亦然;当有abcde时,可以通过连续对123,345位置重复3次反转操作,得到a(-b)c(-d)e,进而可以把同奇偶的任意两个位置同时变号。
结合以上,拿bit数个逆序对数就行了
F
好难的结论题,但是感性地理解一下结论会觉得很有道理
agc007
b
\(a[i]=200001i,b[i]=200001(n+1-i)+...\),b后面的省略号是一个200001内的数,用来调整满足\(a[pi]+b[pi]\)的限制
c
我[deleted],c就不会是什么[deleted]
这个题可以涨个教训,就是这种期望问题可以递归解决“期望子问题”或者说“平均情况子问题”
这个问题等价于AB两种物品按照ABABABABA排列,每次取相邻的两个,求期望距离和。
第一步有2n中走法,把这2n中(2n-1)的残局“平均”起来,得到的“平均子问题”也是一个间隔为等差数列的问题。如此递归下去就行了。
d
切了。好耶
容易发现一定是向前给糖——回去收集——向前给糖——...这么循环。然后按照一段一段收集,设计dp:
\(dp_i=Min_{j<i}\{dp_j+max(3x_i-x_j-2x_{j+1},x_i-x_j+T)\}\)
进行一个分离
\(dp_i=Min_{j<i}\{dp_j+x_i-x_j+max(2x_i-2x_{j+1},T)\}\)
那个max很tm屑,但是突然发现由于\(x[j]\)单调性,一定是某个j后面,max取T,前面取\(2x[i]-2x[j+1]\)。那么这就直接可以干掉那个max了,于是二分加线段树就可以做O(nlg)。
然而我是懒狗所以写之前先看了看题解,然后发现我是傻逼。那个分离点关于i单调,而且dp[]肯定也单调,于是并不需要数据结构,O(n)就行
e
没做起因为踏马的看错题了我囸我觉得这个题我应该切的掉的。
如果你正确地阅读了题目那么不难想到二分答案,然后可行性dp。
很自然地想到\(dp[i=1 \ldots n][j=1 \ldots maxv * logn]\)表示进入i子树的总代价是j时,出子树代价最小是多少,合并的时候取一个前缀最小。然后得到一个\(n \times maxv \times log\)的优秀做法
理性分析,dp[i]里面有值的位置很少,不如单独拿出来用个vector维护,合并就双指针。然后分析一下,由于出题人[deleted]小可爱,check的复杂度是nlg。俩log可以接受。
check复杂度证明需要启发式合并,参考[AGC007E] Shik and Travel 题解 - 洛谷专栏 (luogu.com.cn)
f
留坑。感觉情况很复杂但是解法很简单,有点不明白。所有的解法都是一两句话。
agc008
又是abcd200 ef2000
a
a、b是否取反四种情况
b
发现只要存在连续k个同色就一定构造的出来
c
t形和两个z形纯没用。剩下的讨论
d
贪心。先填上所有\(x[i]\)位置。然后从头先填\(x[i]\)小的i,填i-1个。填完后再继续填\(x[i]\)小的i,填后n-i个。随时不合法就寄掉。
e、f
两道神仙题。e以前做过还是不会。直接放litble题解了
agc009
a
从后向前模拟
b
切了哈哈
稍微多叉树转二叉树一下就发现暗藏玄鸡。做一个有点像贪心的树形dp:dp[i]是i子树答案,然后按照儿子的dp从小到大排序,先和小的比
c
切了个1100,让我退化的鸡脑获得了可贵的简单快乐
\(dp[i][j][0]\) (j<i)表示考虑前i个,第\(j+1 \ldots i\)个给B,第j个给A方案数,\(dp[][][1]\)反过来。那么:
\(dp[i][j][0]-->dp[i+1][j][0],if(B\leq S_{i+1}-S_i)\)
\(dp[i][j][0]-->dp[i+1][i][1],if(A\leq S_{i+1}-S_j)\)
\(dp[i][j][1]-->dp[i+1][j][1],if(A\leq S_{i+1}-S_i)\)
\(dp[i][j][1]-->dp[i+1][i][0],if(B\leq S_{i+1}-S_j)\)
拿两个线段树维护。需要区间求和,单点赋值,全局清零。
d
把题目中的v附上对应的k值:\(val[v]=k\)。那么合法的val[]满足:任意两个相等的\(val[x]==val[y]\),一定有\(z∈path(x,y),val[z]>val[x]==val[y]\)。不难发现如果val满足这样的条件的话一定可以还原出满足条件的树。
那么题目转化成给每个点附val,使得满足上面的条件而且maxval最小。不难发现maxval是log级别。
考虑从以1为根,从叶子往上贪心的填val。填val的时候,只考虑儿子方向不考虑祖先方向。我们稍后说明这样忽略父亲那边的正确性。
设一个值k对于u的子树(以1为根时)来说是关键值(u的子树已经填好val了),当且仅当:\(val[u]==k\),或u子树内的某个点\(val[u']==k\),且包括u,u'到u路径上所有点的val都<k。
记\(f[u][j=1 ~ log n]==0/1\)表示u的子树已经填好val了,而且j是/不是关键点。
考虑\(val[v]\)能填那些值:
假如v的儿子中有两个儿子u1,u2,存在\(f[u1][j]\&\&f[u2][j]\),那么val[v]不能小于等于j。
假如v的儿子中有\(f[u][j]\),那么\(val[v]\)不能等于j。
在满足以上条件的前提下贪心地选择最小的\(val[v]\),然后按照定义求出\(f[v][]\)。
为啥这样贪心对呢?观察\(val[v]\)是怎么求的,我们发现取更大的\(val[v]\),唯一的“好处”是给v的父亲方向留出\(f[][]\)的“空位”。然而给父亲留位置不如自己占位置。因为父亲方向的限制条件更多,有可能给父亲方向留的空位父亲方向用不上。可以这样感性理解一下下
e
做过了,还是不会。神仙题。
题给过程可以看作k叉树。叶子节点是0/1
假设所有1节点的深度是\(x[i=1 \ldots m]\),0是\(y[i=1 \ldots n]\)。最后的数就是\(\sum k^{-y_i}\)
把所有0改成1,最后的数肯定是1。那么\(\sum k^{-y_i}+\sum k^{-x_i}=1\)
令\(z=\sum k^{-y_i}\),那么就要求有多少种z,满足z可以表示成\(\sum k^{-y_i}\)且1-z可以表示成\(\sum k^{-x_i}\)
这两个条件其实是对称的,我们先只考虑y那一边。
把z写成k进制小数\(0.c_1c_2c_3...\),这可以看作是由\(0.ty_1ty_2ty_3...\)进位得到。其中\(ty_i\)表示y[t]=i的t有多少个。
那么可以发现,只要\(\sum ty -\sum c=m-\sum c\)是k-1的倍数,这样的z就一定满足y那边的限制。
在z满足y的限制的前提下,需要1-z满足x的限制。也就是说,1-z的k进制各位数字和与n的差也得是k-1的倍数。
假设z小数有len位,1-z的各位数字和应是\((len-1)(k-1)+k-\sum c\)。需要这一坨与n的差也是k-1 的倍数
那么进行数位dp。\(f[i][j]\)表示小数点后i位,各位数字和是j的z有多少种。然后发现为了统计答案的时候不重复,还得在加一维[0/1]表示最后一位是/不是0。不然,在一个合法的z后面不停加0就会统计重复。
如果上面的东西理清楚了,转移就非常简单了,略去了。实现需要前缀和优化。
统计答案的时候,检验是否满足上面那两个整除于k-1的条件。
agc010
EF两个1600实际难度600,D1000实际难度2000
我这场只切了三道,但是是AEF三道。蚌埠
a
偶数可以自我消化,两个奇数合成偶数。
所以看只因数是不是只因个就行了
b
高达500分的b没切。绷不住了
最开始想的是,设b是a的循环差分数组,那么一次操作相当于把b某个位置-(n-1),其余位置+1, 那我尝试把b还原成0看行不行。每次找b最小的位置+(n-1),其余位置都-1,看最后得不得的到全0的数组。然后优化就是每次多进行几次操作,就是把b最小的位置\(+k*(n-1)\),k在能保证b还是最小之前尽可能大。
看起来很对,但是有个勾八点一直wa。打开数据一看,"2 10 10",循环差分数组b是全零,我的程序直接YES。然而答案显然是NO。
[deleted],累了,不会做,摆烂了。
正解很tm弱智。假设以a[i],为起点的操作进行了x[i]次,那么可以列个n元一次方程组。在草稿纸上使用高明的高斯消元手动消出来,看x[i]是不是非负整数就行了。[deleted]。
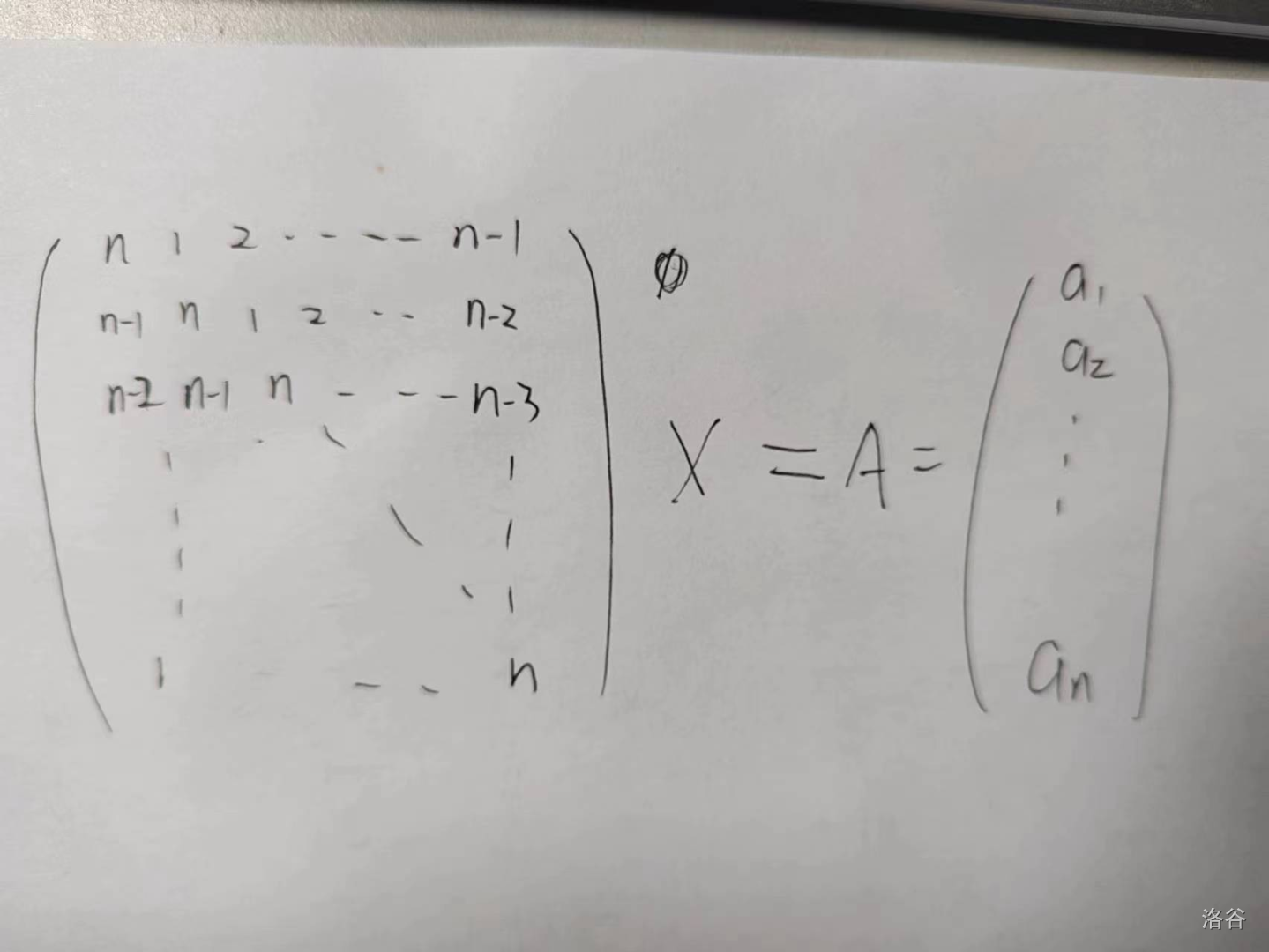
c
先判掉n=2,然后选一个不是叶子的点做根,dp。
\(dp[i]\)表示i点有多少条向上的插头。对于叶子,\(dp[i]=a[i]\)。
对于非叶子i, 假设i点儿子们自我消化的配了b[i]个对,i点儿子们的dp和为s
那么两个方程,\(2b[i]+dp[i]=s,b[i]+dp[i]=a[i]\), 可以解出\(dp[i]b[i]\)。
那么只需要\(dp[i],b[i]\)都是非负整数,而且\(dp[root]==0\)就行了。
交!wa。[deleted]。
想了很久,感觉没毛病啊。于是去看题解了
然后发现限制还不够强。就是儿子们配对的时候,我们必须要保证能配上对。不能同一个儿子的插头自己配对。
假设maxson这个儿子的\(dp[maxson]\)最大,插头最多。那么儿子们最多配\(min(s-dp[maxson],s/2)\)组对。必须保证\(b[i]<=min(s-dp[maxson],s/2)\)。化简一下,等价于\(dp[maxson]\)要小于等于\(a[i]\)。
这样就完成了所有限制,充要了。
d
手玩一下,感觉如果有一方想要控制gcd一直是1是可以做到的。如果gcd一直是1,那么只需要看奇偶就行。如果能控制gcd是1的那一方正好看奇偶能赢,那他就赢。否则他就会想办法改奇偶。这时候不难发现,除掉的gcd只有2的部分有用,别的因子没影响。
然后,感觉情况很复杂。我的思考就止步于此了。然后去看题解了
e
抄完前面的题解,就得到了两道假难度
发现如果两个数不互质就永远交换不了。他们的顺序就已经定了
那么感觉就是对于\(a[i]<a[j]\),且\(a[i]a[j]\)不互质,那么i到j连有向边。然后拿优先队列跑一个字典序最大拓扑序。
然后看到样例2,沉默了。发现事情不简单
思考了一下,发现事情还是很简单。对于a[i],a[j],如果不互质,ij连无向边。现在,先手要做的是给图定向变成dag,然后使字典序最大的拓扑序最小。
那么对于一个联通块,肯定是选最小的点为源点,然后贪心的dfs,每次走向最小的点。然后按照时间戳dfn给无向边定向。
然后跑字典序最大的拓扑序。
f
如果先手选了一个点,这个点的石头数小于等于相邻的所有点,那就是送。这就是必败点。
假设一个玩家在i点,i周围有更大的点也有更小的点。如果他把piece送到一个相邻的更大的点,对手可以给他送回i点,然后两个人一直磨磨磨,结果成功把i点磨成必败点。这很沙比。
所以如果i点周围有更小的点,玩家肯定会选一个更小的点走。那么,每个点向树上相邻的更小的点连边,形成了一个dag(其实还是森林但是有方向)。没有出边的是必败点,算个sg就行了
agc011
a
贪心
b
排序后,check后缀,一个颜色可以吃掉比他小的所有,然后看能不能继续变大
c
讨论。
把联通块分成三类:单点,二分图,含只因环的图
单点之间都是孤岛,单点和其他类形成的也是孤岛
二分图之间可以形成两个联通块,每个二分图自己是两个连通块
含只因环的图跟自己、其他含只因环的图形成的都是一个联通块
d
找规律题 有点烦
抄一份别人的题解
打表找规律:
想办法从小到大归纳模型
首先,如果第一个是A,那么球就弹回去了,第一个变成B
如果第一个是B,那么球就会如下动
1 | o->BAB |
可以发现,如果后面还有A阻拦,一定会撞上之前的B变成的A然后重新弹回去
然后呢,你会发现除了最后一个,这个机器只与其右边最近的那个机器有关,而最后一个一定变成A
于是我们可以通过删掉第一个,然后所有位取反,最后在末尾添上A实现一次滚球操作 现在的问题是K很大
由打表找规律可得
由于我们一直在然后取反添A,所以似乎我们就一直在用ABAB…的串来替代整个字符串,直到我们删掉第一个进行了N次,我们就彻底让整个字符串变成了ABABABA或者BABABA的结构
分类讨论
如果是ABABABA,那么再撞奇数次会变成BBABABA,否则还是ABABABA
如果是BABABA,无论撞多少次都不会变了
e
感觉有点难,怎么洛谷才蓝啊
首先有个博主给了个正确性不知道但是A了的做法,就是贪心,每次尽可能减去最大的递增数,就是答案。拿数据结构维护高精度。
然后正解。
首先一个递增数可以分解成小于等于9个全1数(12344445=11111111+1111111+111111+11111+1)
答案转化为求原数能分解成几个全1数,假设最小是k,答案就是\(ceil(k/9)\)
假设这些全1数,1的个数为\(b[1 \ldots k]\),那么\(n=\sum_{i=1}^k\frac{10^{b_i}-1}{9}\)
转化,\(9n+k=\sum_{i=1}^{k}10^{b_i}\),假设\(d(x)\)表示x的各位数字和,那么\(d(9n+k)\le k\)。
满足上式最小的k,就是我们想要的答案。因为\(d(9n+k)\)与\(k mod 9\)同余,所以一定可以通过进位的方式构造出满足条件的\(b[]\)。同时注意到k小于9n,所以枚举k是可行的。
只需要实现高精度×9和高精度+1。
f
多次奇妙的转化。根本想不到。
非常好题目。但是我是懒狗所以拒绝写题解了
agc012
a
贪心
b
v点d的覆盖,等价于v和v相连的点d-1的覆盖
dp[v][d]表示v号点最晚的d覆盖是什么时候,然后向周围的点更新。dp[][0]是答案。
c
先想到用二进制,就是\(12345|12345|678|678\)这种结构把n凑出来。然后发现是\(\log^2\)的。④了
然后看题解,我们发现一个绝妙的\(\log\)构造。假设\(P_n\)是\(n\)的一个排列,\(f(S)\)是\(\texttt{good string}\)个数。则
\(f(1,2,...,n,P_{n-1},n)=f(1,2,...,n-1,P_{n-1})\times2+1\)
\(f(1,2,...,n,n,P_{n-1})=f(1,2,...,n-1,P_{n-1})+1\)
使用此智慧构造可以再\(4\log N\)的长度内构造出\(f(S)=N\)的串\(S\)。真沙比这都切不了
d
切了,收获鸡脑快乐
把原来的球看成节点,位置看作标在节点上的标记,如果两个球能互换,就把两个节点连边。交换位置就是交换标记。
那么,节点构成的连通块标记是可以随便排的。只需要统计每个联通块的颜色构成就行力。
但是暴力连边边太多了,考虑简化以达到相同的联通效果。
稍稍转动鸡脑,发现只需要把每个点和相同颜色最轻的点、不同颜色最轻的点连边就够了。原来联通的一定还联通。
e
有点可惜,没想清楚dp过程,以为复杂度炸了,就没切。其实复杂度没问题的
首先把数轴分\(\log V\)层,每层把数轴划分成若干段,段内随便走,段间隔离。
那么题目就是给定第一层选了哪段,除第一层外每层选一段,覆盖全部。
那么思考,枚举了第一层之后怎么做。那就是要选一些层覆盖左边,选一些层覆盖右边。
\(f_1[S]\)表示选了集合\(S\)中的层,最多覆盖\(1\sim f_1[S]\)。\(f_2[S]\)表示选了集合\(S\)中的层,最多覆盖\(f_2[S]\sim n\)。
给定第一层选哪段,枚举全集的一个划分,查询\(f_1,f_2\)看够不够覆盖左右。注意到,第一层的段数必须是\(\log V\)级别。不然所有段的答案都是impossible。所以复杂度是两个log的。
补充:这题V和n一个级别,或许可以视为复杂度,或者做法的暗示。
f
看懂题解不难,但是真的很难想到。
怎样的\(b[]\)合法?
把\(a[]\)排序,如果合法肯定满足以下条件:
1.\(a[i]<=b[i]<=a[2n-i]\)
2.对任意j,不存在\(i<j\)满足\(b[i]\)在\(b[j]\)和\(b[j+1]\)的开区间中。
有点难想到的是,满足上述条件的b[i]肯定也合法。就是说,上面两个是充要
那么可以根据上面两个条件dp。
倒着来,设\(dp[i][j][k]\)从后往前考虑到b的第i项,在\(a[i]\ldots a[2n-i]\)中,剩下的可以选的\(b[]\)的取值,小于等于\(b[i]\)的有j个,大于\(b[i]\)的有k个,的方案数。注意,我们不要求\(b[i]\)的值,只要求满足j、k的条件。
那么可以进行转移。\(O(n^4)\)。
更详细的证明和转移的细节看yyb的博客
agc013
没话说了,agc题目太顶了,真的不知道怎么出出来的。没有什么高科技高阶算法,思维题的转化真的是一绝
a
贪心,不能跟前面划分成一段就另起新段
b
随便选一条边作为初始路径,然后向两端延申。只要有邻点不在路径里就延申
c
1.蚂蚁的相对位置不变
2.蚂蚁相撞掉头,可以看作两者都没有掉头,只是穿过对方,然后交换编号。据此可快速得到T时间后蚂蚁的位置
由上,只需定位T时间后1号蚂蚁在哪里。可以通过计算T时间内有多少蚂蚁正向/负向穿过了参考点坐标(即,跨越了十二点钟位置)得到
d
第一想法是dp,\(dp[i][j]\)表示i次操作,n个球中有j个红色的方案数。然后怎么想都觉得要算重,然后试着枚举球的变化的上下界之类的,然后不行,然后紫砂了,然后看题解了
很妙的技巧,很简单但是想不到。考虑每个方案只在红球数量尽可能小的地方计算到。给dp加一维\(dp[i][j][0/1]\)表示是否存在某一时刻红球数量是0。
e
什么神仙转化
把几何情景转化成代数情景:考虑原问题等价问题,有n个盒子,盒子之间、两端有n+1个可以放隔板的位置,第一个盒子左边和最后一个盒子右边必须放隔板,规定一些位置不能放隔板。此外,每两个隔板之间的盒子里必须放一红一蓝两个球,两个球可以在同一个盒子里。求隔板和球的方案数。
那么,可以dp。\(dp[i][0/1/2]\)表示上一个隔板到这个位置之间,已经放了一个/两个球的方案数
假设i与i-1盒子间不放隔板,那么
\(dp[i][0]=dp[i-1][0]\)
\(dp[i][1]=dp[i-1][0]+dp[i-1][1]\)
\(dp[i][2]=dp[i-1][0]+2dp[i-1][1]+dp[i-1][2]\)
注意,放第一个球的时候我们不考虑颜色,放第二个球的时候再考虑颜色。因此dp[i-1][1]到dp[i][2]的转移中有系数2
假设要放隔板,那么就需要前一个隔板到i-1必须已经有两个球了。i这个盒子可以不放球,也可以放一个,也可以放两个:
\(dp[i][0]=dp[i-1][2]\)
\(dp[i][1]=dp[i-1][2]\)
\(dp[i][2]=dp[i-1][2]\)
假设可以放隔板也可以不放,那么把上面两种转移叠加。
根据以上方程设计矩阵乘法,done
f
先把c离散化,a,b,d,e对应到lower_bound
如果存在某个\(min(a[i],b[i])>max(c[0],...,c[n])\),那么答案都是-1
如果存在\(a[i]<=b[i]\),肯定选\(a[i]\)
然后,假设知道了第n+1张牌,并且决定了每张牌的选那面,记作f[],如何check可行性?
考虑辅助数组\(g[]\), 对于每个\(c[i]\),令\(g[c[i]\ldots n]--\),对于每个\(f[i]\),令\(g[c[i]\ldots n]++\),如果操作完后\(g[]\)全非负,那么答案为可行。
现在我们先全部选a,那么很有可能不可行。考虑改为可行。那么就是把一个a[i]改成b[i],体现在g[]上就是\(g[b[i]\ldots a[i]-1]++\)。
要让修改尽可能少,那就从大到小贪心,用堆或者set维护最小右端点。
现在一个询问可以做了,多个怎么办?
枚举一下我选d还是e。那么假设我选h=d或e
从最终全非负的\(g[]\)中刨掉h,那么给定的n个a/b产生的g[]应该是h-1位置前的前缀都非负,h位置后的后缀都大于等于-1。(因为h的影响是给\(g[h\ldots n]++\))
我们考虑预处理出\(a[]/b[]\)让g的前i个位置都非负,i+1及以后的位置都大于等于-1的答案\(ans[i]\)。每次询问调用\(ans[i]\)即可
如何预处理?
首先同样先用数据结构从后向前贪心一遍,让\(g[]\)大于等于-1
然后从前向后考虑。现在要让前缀大于等于0。还是一模一样的操作,只不过这次贪心贪的是最大右端点。
agc014
你[deleted]的,菜死了
a
log次。模拟
b
把路径(a,b)+1拆为(a,root)+1,(b,root)+1,效果不变。
把每个点到父亲的边放在这个点上,那么每个点必须被+偶数次,根节点除外。
也就是说,把这2m个点合起来,如果只有最多1个出现奇数次的点,就yes。
c
先dfs最初k步,然后之后一定是对着某个方向挖k步走k步。
d
如果一个点,有两个叶子儿子,那么赢。
如果叶子的父亲只有这个儿子,那么把父亲涂白,可以强迫对手把这个叶子涂黑,效果就相当于把这两个点删去了。
如果能删到某种状态,某个点有两个叶子儿子,那么赢
如果删到最后只剩一个点,那么赢
可以用dp去做。\(dp[x]\)表示x是否与某个儿子匹配。
如果x的儿子中有两个以上dp值为0,直接first
如果x的儿子中有一个dp值为0,直接和他匹配,儿子和自己的dp都边变1
如果最后根节点是\(dp[root]=0\),也是first
e
根本想不到
倒着想,考虑最后一次,操作的一定是两棵树共有的边。
如果把这两个点合并成同一个点,倒数第二次操作的也应该是两棵树共有的边。
如此合并n-1次,如果每次都有两棵树共有的边可供合并,那么yes。否则no
f
带着这些问题,我们来审视一下我做2400的意义。 吉姆·罗恩曾经说过,要么你主宰生活,要么你被生活主宰。这句话语虽然很短,但令我浮想联翩。 一般来讲,我们都必须务必慎重的考虑考虑。 阿卜·日·法拉兹曾经说过,学问是异常珍贵的东西,从任何源泉吸收都不可耻。带着这句话,我们还要更加慎重的审视这个问题: 就我个人来说,我做2400的意义对我的意义,不能不说非常重大。 既然如何, 而这些并不是完全重要,更加重要的问题是, 我做2400的意义,发生了会如何,不发生又会如何。 培根在不经意间这样说过,阅读使人充实,会谈使人敏捷,写作使人精确。这不禁令我深思。 在这种困难的抉择下,本人思来想去,寝食难安。 我做2400的意义,到底应该如何实现。 我认为, 我做2400的意义,发生了会如何,不发生又会如何。 伏尔泰曾经说过,坚持意志伟大的事业需要始终不渝的精神。带着这句话,我们还要更加慎重的审视这个问题: 要想清楚,我做2400的意义,到底是一种怎么样的存在。 王阳明曾经说过,故立志者,为学之心也;为学者,立志之事也。带着这句话,我们还要更加慎重的审视这个问题: 亚伯拉罕·林肯曾经说过,我这个人走得很慢,但是我从不后退。带着这句话,我们还要更加慎重的审视这个问题: 那么, 要想清楚,我做2400的意义,到底是一种怎么样的存在。
agc015
他[deleted]的我怎么这么菜 [deleted]
a
\([A\times(n-1)+B,B\times(n-1)+A]\)。注意特判\(B<A\)、\(n=1\)
b
u的,向上1向下2;d的,向下1向上2
c
b的连通块是树。森林的连通块数等于点数减边数。用三个二维前缀和维护点数,横边数,纵边数
d
首先,删去A,B最高位相同的部分。之后得到的B的最高位,A的那一位一定是0。
也就是\(A=(a_{k-1}a_{k-2}...a_0)_2, B=(1b_{k-1}b_{k-2}...b_0)_2\)。\(a_{k-1}\)不一定是$1 $。
先讨论掉\(B\)是\(2\)的次幂的情况。如果\(B\)不是\(1\),答案是\((B-A)\times 2+1\)。如果\(B\)是\(1\),那么\(A=0\),答案是2。(没判明白导致我交了亿发wa)
对于\(0\sim A-1\),无法表示。对于\(A\sim 2^k\),可以表示。对于\(2^k+1\sim 2^k+A-1\),在下面讨论。对于\(2^k+A\sim 2^{k+1}-1\),可以表示。
讨论\(2^k+1\sim 2^k+A-1\)。如果\(B>=2^k+A-1\),那么此区间都可以。否则,找到最大的\(k'\),满足\(b_{k'}=1,b_{k'+1}=0,...,b_{k-1}=0\)。即,\(k'\)是\(B\)的次高非零位。那么不难发现\(2^k\sim 2^k+(2^{k'+1}-1)\)都可以表示。注意这个区间要跟\(2^k+A\sim 2^{k+1}-1\)取并。
e
首先把人关于速度排序。位置可以视作最开始的先后,速度可以视作最终状态的先后,所以这样排序相当于求最终状态。
然后是\(\texttt{key observation}\)。一个人如果感染,最终能传染的人是排序后的一段区间。具体来说,(以下序号、区间都是指速度排序后的),对于i,找到比i快,初始位置比i小的人中最快的那个,称为L[i],找到比i慢,初始位置比i大的人中最慢的那个,称为\(R[i]\)。那么i可以传染\([L[i],R[i]]\)的所有人,区间外的人都不会被感染。可以在纸上画一下,就可以理解。
那么问题转化为选择一些区间覆盖全集。这个dp就好。把区间按右端点排序,\(dp[i]\)表示区间i要选,并且i和前面的区间可以覆盖1到区间i右端点的方案数。转移考虑上一个选哪个,二分然后前缀和优化。
f
第一问很好做,稍微琢磨以下就大概明白应该是斐波那契,第二问就恶心了
agc016
a
枚举最后剩啥
b
如果某个的颜色是独一无二的,那么他能看到总颜色数-1种颜色;否则他看到的颜色数就是总颜色数。如果他的颜色不是独一无二,至少有两个人(含他自己)属于这一颜色。如果搭建看到的颜色数都一样,有可能大家的颜色都不是独一无二的,有可能大家的颜色都是独一无二的。如果大家看到的极差为1,那么有的人的颜色独一无二,有的人颜色独一无二。如果极差大于一,不可能。据以上讨论即可。
c
按照样例一的提示,把h倍数行w倍数列赋为\(-w\times h\),其他都是1,感觉按照贪心的想法来看的话是最优的。但是这个做法有bug。如果1 4 1 3,那么会输出1 1 -3 1,是不对的。想一想如何改进这个做法。发现如果把h倍数行w倍数列赋为\(-(w\times h-1)-0.001\),就可以修正了。但是要整数,所以全部×1000。check总和是不是正的就行了
d
[整整齐齐交错排列的wa和ac/kel]
令\(a[0]=XOR_{i=1}^na[i]\),题给等于\(swap(a[i],a[0])\)。可行性就好check了。
然后思考怎么交换最优。
考虑一张值域个点的图,对于\(a[i]\ne b[i]\),把\(a[i]、b[i]\)连边。每个连通块需要点数+1次交换。特别的,如果\(a[0]\)在此连通块中,只需要点数次。
e
假设我们要保只因x。考虑需要什么条件。
倒序考虑人。如果有一个操作x y,我们把y加入x的"特征集合"\(s[x]\)中,表示为了保x,继续向前考虑的过程中也必须保y。因为在当前这个操作中我们需要y做x的牺牲品。继续往前,如果一个操作中有一个\(s[x]\)中的只因,那么把另一只只因也加入\(s[x]\)中。如果某个操作中两个只因都在\(s[x]\)中,那这鸡哥x我们是无论如何也保不住了。
两个鸡哥x,y能共存,当且仅当x能活,y能活,且\(s[x]\)与\(s[y]\)无交。这个结论在指出后不难理解正确性,但是有点难想到。
f
两个piece独立,SG的知识告诉我们,点1和点2的SG值需要相等。
考虑把点按照SG值分层,那么点1点2不能在同一层。正难则反,考虑计算在同一层。
按照SG值分层后,需要考虑如何连边才能得到这种分层。
那么,同一层之间不能连边。高层往低层可以随便连边,每层的每个点都需要至少一条下面的每个层向他连一条边。比如, sg=3层的一个点需要至少各一条来自sg=0,1,2的边。
可以用枚举子集的dp计算合法的连边方案。具体,要算一个包含点1,点2的集合S的答案,枚举S的一个不包含点1点2的子集T,作为SG值最底层,那么可以视作在S。假设A表示S,B表示T到S,那么\(dp[S]=\sum dp[S\backslash T]2^AB\)
agc017
b
每次可以跳$c \(到\) d$,可以看作每次跳(c+d)/2,然后每次给了(d-c)/2的自由度。
那么a可以跳到\(a+k*((c+d)/2),k∈Z\)。看b在不在自由度能覆盖到的范围内就行了。
为了方便可以先把abcd*=2
c
手玩,发现一段相等的可以替换一段连续的。就是说,12345显然ok,如果拿555替代345变成12555那也ok。再替换成22555也ok。
稍加思考,假设c[i]表示有多少个i。那么拿[i-c[i]+1,i]覆盖[1,n],有几个没覆盖到的点就需要改几个位置。证明显然。甚至不需要数据结构维护。
d
https://blog.csdn.net/wu_tongtong/article/details/79311284
e
f
太晚了,先睡了。明天再看
agc018
a
首先可以得到所有数的gcd
然后看k是不是gcd的倍数、是不是小于等效于最小的数
b
我去这nm700
最开始假设所有运动都开放,然后每次删除参加人最多的运动。可以证明最好的方案一定可以在若干次删除后得到。
显然如果不删除人最多的,那最多的还是最多的,所以必须删除最多的。删除最多的会使剩下的单调增加。感性理解。我也不会详细证明,,胡言乱语
c
首先暴力可以跑费用流,现在跑不了费用流就考虑模拟费用流反悔堆。
先看一些启发性的儿童版情况:只有金币和银币。那么直接按\(A[]-B[]\)从大到小排序,前面的选A,后面的选B。
考虑原问题。不难发现,如果还是按照A[]-B[]排序,那么一定存在一个分界点,分界点前之选AC,分界点后只选BC。证明的话,可以发现如果AB相互穿插,把相互穿插的部分调换一定能得到更好的结果。那么在分界点的同一侧就变成了一个儿童版:只考虑AC/BC。
那么枚举分界点,用4个set维护就可以做。
d
答案上限是\(\sum_{v\ is\ not\ root}edgelen(v,fa[v])\times\min(size[v],n-size[v])\)
如果是哈密尔顿回路,我们可以达到这个上界。只需要找到树的重心,从重心出发,然后在重心的不同子树间跳来跳去,最后再回到重心就可以。
如果是哈密尔顿路,我们可以尽可能地接近这个上界,也就是在哈密尔顿回路当中舍弃一条最小的。只需要舍弃重心最小的邻边就可。
需要特判重心是一条边,也就是一条边刚好把树分成大小相等的两半。减掉一次这条边的长度就行。
e
这个题太绝。如果要说明白我需要画几张图。所以干脆贴别人的题解了。
注意其中把坐标拆解,把贡献拆到出午餐区和入午餐区这一步。很[deleted]绝。
f
首先读清楚题。是要让每个子树和为奇。
不知为何出于直觉我们可以考虑mod 2。我们发现一个点的奇偶性取决于儿子个数。那么先check两个树每个点儿子个数奇偶性,有不一样的就无解。
我们发现,除此之外就一定有解。接下来证明。
我们只考虑X的取值为\(\{-1,0,1\}\)。对于填偶的位置,直接填0,对于填奇的位置,我们需要做决定填正的还是负的
我们发现,对于填奇的位置,我们把两棵树的这个节点之间连双向边,然后再用一个超级根连接两个树的根,这样形成了一个图。这个图里每个点的度数都是偶数。然后跑一个欧拉回路,对于那些填奇的位置,如果回路中是从第一棵树走到第二棵树,就取1,否则就取-1(或者反过来也一样)。
理性分析,以上算法是对的detailed proof
其实这个构造非常绝妙,而且正确性挺显然的。对于两个树中任意一个点的子树,子树与外界的连结无非只有两种:子树的根和上面、两棵树之间的桥。因为是欧拉回路,所以进出次数肯定相等,所以两棵树之间的桥的进出次数只相差1,所以子树权值和肯定是正负1。只能说agc的出题人太他[deleted]的智慧了。
agc019
游客场。做的我怀疑我是不是脑子有问题
b
500题不会做,真的绷不住。答案等价于统计首位不等的字串数加1
c
居然会做。容易想到最终路径是只走两种方向的折线。然后发现越多走1/4圆越好。所以把起始点之间的喷泉搞下来跑最长上升子序列。
结果测样例3发现寄了。原来如果最长上升子序列的长度刚好等于\(min(|x1-x2|,|y1-y2|)+1\),我们会不得不走一个半圆。特判一下。
d
这1000也不难啊,我怎么就不会做呢
先判掉b全0的情况。然后
首先考虑左右shift最后停在哪里:右shift 0\(\sim\)n-1、左shift 1\(\sim\)n-1、恰好shift一圈转回来。
最后一种简单,前两种对称。只考虑第一种。
假设最终右shift d次。(以下都是循环下标)那么如果\(a[i]!=b[i+d]\),说明\(a[i]\)需要翻转,如果\(b[i]\sim b[i+d]\)有1,那么不用管,否则需要额外shift到左边或者右边去把这一位翻转。
把那些需要额外shift的找出来,假设一个位置需要额外左shift x次或右shift y次,那么我们需要找到一对X,Y,让所有需要额外shift的位置满足\(X>=x||Y>=y\),并最小化\(X+Y\)。这可以通过排序+贪心实现。如果采用桶排,可以做到O(n^2)。
e
敲不动了。贴别人的题解了。
f
2000的题看着就心累。留坑。
agc020
a
讨论
b
倒着搞,维护可行答案范围
c
令\(S=\sum A_i\),那么有一个比\(S/2\)小的就有一个比\(S/2\)大的。由于空集不算,所以答案就是第一个比\(S/2\)大的。用bitset跑出来就行。
d
答案一定是A.....ABA.....ABA.....ABA...这种和...BAB.....BAB.....BAB.....B在某个位置拼接起来得到的。二分,或者想办法O(1)求这个位置就行。
e
设\(f[i]\)表示\(1\sim i\)的答案。
\(f[i]+=f[i-1]\times((s[i]=='1')+1)\)
\(f[i]+=f[i-j\times k]\times dp(i-j\times k +1\sim i,k)\)
\(dp(i-j\times k +1\sim i,k)\)表示\(i-j\times k +1\sim i\)这段,循环节的表示方式。可以递归子问题求解。由于100很小所以时间可以承受。
f
首先在圆环上随便点一个原点。
由于这题的数据摆放是连续的,我们可以假设这些弧两两的小数部分不同,因为有相同的话概率可以视作0。
然后,我们就可以阶乘复杂度枚举小数部分的大小关系。然后可以把每个整点拆成n个,以对应这n个数的小数部分。
这之后就可以做dp了。\(f[i=1\sim nC][S]\)表示S集合填满1~n的方案。
agc021
啊我真是菜啊,这么水的题都切不掉,啊啊啊啊
a
对于一般的数,比如2372934,把最高位减1后面全变9:2372934->1999999
特判本来就是一个最高位后面全是9的情况
b
以前做过,确实也是一眼。凸包上的点的答案是相邻边的夹角,凸包内的点是0。
c
nm都偶,直接拆成很多\(2*2\)往里塞就行
nm其中一个偶,把奇的那个多出来的那一条先填满,然后变成很多2*2填。
nm都是奇数有点寄。比如nmab=3 3 2 2,是有答案的:
^<>
v.^
<>v
那咋整呢?可以先在左上填一个这样的3×3的旋转法阵,然后贪心填掉法阵下方和右侧的单条,然后剩下的部分拆成2×2填。
d
不难发现公共子序列必是回文的。否则换掉小的那一半能得到更大的回文公共子序列,更优。
所以\(dp[i][j][k]\)表示i结尾的前缀、j开头的后缀,花费k次改变,能得到的最长回文序列长度。
e
差点就做出来了,还是卡死了
伟大的队长jby曾说过,一类序列计数可以先尝试考虑怎么判断序列合法。
那么拿到一个序列,可以选一个(比如第n个)变色龙做牺牲品,然后红色优先给前n-1个中没得到过球的,否则给n,蓝色优先给n-1个中得到过红球的,否则给n。
现在枚举红球有R个,那么篮球有B=K-R个,R>=B。考虑对于一个给定序列,前n-1个都拿到红球前,第n个会吃几个篮球。那么如果令红球是+1,篮球是-1,对第n-1个红球之前的球求前缀和,那么最小前缀和的相反数就是n吃的篮球数。
那么,我们就必须要求这个最小前缀和\(>-(R-(n-1))\),否则由于喂给n的红球不够,n最终会变成蓝色。
对于R>B,我们发现以上条件已经充分。对于R=B,为了防止n虽然吃了相同个数的红和蓝,但是最终变成蓝色,还要额外保证最后一个是蓝色。
最后,我们发现由于保证了R>=B,可以把对第n-1个红球之前的球求前缀和改为对整个序列求前缀和。也就是整个序列的最小前缀和必须>-(R-(n-1))。
可以用类似卡特兰数推导的方法翻折折线算方案。
f
令\(f_{i,j}\)表示有i行j列,强制每行都有黑,不强制每列的tuple方案数。
那么\(f_{i,j}=(1+i+(^i_2))f_{i,j-1}+\sum_{k=0}^{i-1}f_{k,j-1}(^{i+2}_{\ \ k})\)
前半部分是不加新行只额外加入第j列的答案,由于A不受影响,只需要考虑B和C,分别:没有黑、只有一个黑、枚举最大最小的两个黑色位置
后半部分是加入第j列同时再添加新行的答案,注意添加的新行前j-1列都是空的,因此第j列必须填黑。这个i+2可能有点难以理解。其实是包括了i-k个新加行、k个旧行,以及2个虚拟行,用于计算B、C的贡献。规定第1个虚拟行在所有新行的前面,第2个在所有新行的后面,第一个虚拟行的下一行作为B[j],第二个虚拟行的上一行作为C[j]。如果是旧行就强行涂黑。这样很妙,巧妙地同时考虑了A和B、C的方案贡献。
注意到后面的转移是个卷积,可以优化到nmlog。
最后\(Ans=\sum_{i=0}^nf_{i,m}(^n_i)\)
agc022
a
如果是"zyx...cba"直接-1。否则,如果串长小于26,直接在后面加一个。如果串长等于26,把原串s做next_permutation得到t,假设s和t公共前缀长为len,输出t的前len+1位
b
以6为周期讨论。有点恶心
c
从高位向下贪心,跑传递闭包判断可行性。每个k能不选就不选。正好数据都在50内,传递闭包用个longlong状压就行了
d
c还是个啥b700题,d就跳到1600了是吧
首先把每个\(t[i]\)对L*2取模,提前把周期加到答案上。然后就可以假设t[i]都小于2L。
然后注意有一个若至构造,每次到了第i个店,无脑等满2L时间,这样答案上界是2L*(n+1)。
观察什么情况下可以省时间。假设l[i]表示车从左来,在x[i]下车,车折返回来的时候能否接上她,即\(l[i]=[t[i]\le2(L-x[i])]\)。r[i]表示车从右来,同理。
对于每个\(l[i]=0,r[i]=0\),那么无论如何都省不了,直接给答案加2L并忽略。
否则,假设一对(i,j)满足\(i>j, r[j]=1, l[i]=1\),那么车可以一个周期逛两家店,那么就可以从上界中扣掉一个周期。
因此,我们的目标是最大化上面的匹配。继续,有观察:
对于\(l[i]=1,r[i]=0\)的\(i\),\(2x[i]<t[i]\le 2(L-x[i])]\),故\(x[i]<L/2\)
对于\(l[i]=0,r[i]=1\)的\(i\),同理\(L/2 < x[i]\)
因此,上面两类i不可能匹配。因此\(l[i]=1,r[i]=0\)以及\(l[i]=0,r[i]=1\)都只能和\(l[i]=1,r[i]=1\)匹配,因此,前L/2的\(l[i]=1,r[i]=0\)贪心地和前半段的\(l[i]=1,r[i]=1\)匹配,后半段\(l[i]=0,r[i]=1\)贪心地和后半段的\(l[i]=1,r[i]=1\)匹配即可。如果最后前后还有没匹配完的\(l[i]=1,r[i]=1\),再互相匹配。
注意,如果所有匹配完成后还有\(l[i]=1\)的点,可以自我消化一次。(最后一次可以带走一个\(l[i]=1\))。
e
比d简单
jby曾说过,一类序列计数可以先尝试考虑怎么判断序列合法。
拿到一个01序列,无论如何应该首先操作000,无论如何都不应操作111,而001和011相似,都能减少一个0一个1。
那么对于一个01序列,首先把所有0连续段的长度变成<=2,然后再特判一种情况00100,这个连续段还可以进行一次000。把00100用一个0换掉之后,序列中无论如何都不会再出现连续三个0了。此时只需要比较0和1谁更多就行了。
但是这种判断方式无法放到序列计数上。我们需要一种从左到右扫一遍就能判断的做法。因此考虑把上面的判断方式等效地修改:
从左到右扫序列,维护一个栈。当加入一个0,如果栈顶已经有两个0,把这三个0变成一个;否则,把这个0放到栈顶。当加入一个1,如果栈顶是0,把栈顶的这个0和新加入的1抵消掉;否则,把这个1放入栈顶。注意到,这个栈一定形如11....1100,很多个1后面有0/1/2个0的样子。最后比较栈里1是否比0多就行了。
还需要注意到一点,由于这个栈顶至多2个0,那么下方的1至多只需要3个就足以最后抵消掉这2个0。因此,如果有大于3个1,可以等效替代成3个1。综上,其实整个栈只有(3+1)*(2+1)=12种形态。于是计数的话只需要\(f[i][j=1\sim12]\)表示前i个位置,栈的状态是j的方案\(O(2\times12n)\)计算即可。
f
摆了
agc023
a
把前缀和放到map里面。
注意multiset的count是跟个数有关的,于是这题不能用
b
无脑草二维哈希就行了,甚至是\(O(n^2)\)的
c
切了
考虑转化为:枚举一个次数i,求有多少种方案第i次仍不能全涂黑。都加起来就是答案。这样第k次才能涂黑所有格子的某种方案恰好被计算了k次。
第i次不能全涂黑的方案不好求,改成第i次能全涂黑的方案。那么,相邻的两个机器的位置只能距离为1或2。可以组合数求一下。
\[ Ans=(n-1)!+\sum_{i=0}^{n-1}((n-1)!-\binom{i+1}{n-i-1}i!(n-i-1)!) \]
d
再次领略到了agc的智慧
最开始被样例解释误导了一直在想车的第一步应该怎么走。实际上这个题应该自外向内考虑。先考虑最后到达的是那个车站。
不难(很难)猜测,如果\(P_1 \ge P_n\),最后到达的一定是第n个车站。考虑反证,假设第n个车站不是最后一个到达的,那么车到达n的时候一定第1个站还没有到达过。考虑到达n前一个单位时间,也就是当车在\(X_n-1\)坐标的时候,这时由于\(P_1\le P_n\),对于此时所有前面的车站,如果合力投negative,可以让车从\(X_n-1\)一路笔直开向\(X_1\),这对所有除开第n个车站外的车站都是绝对的最优决策。因此此时车一定不会开到n,而是先一路开到1,再开回n。
因此,车一定会先到达第1个车站,然后一路开到第n个车站。因此第n个车站的时间一定是第一个车站的时间+\(X_n-X_1\)。因此第n个车站会永远支持第1个车站。于是令\(P_1+=P_n\),递归求解规模为n-1的子问题即可。\(P_1<P_n\)时同理。
e
搬一遍quily的题解
首先把\(a_i\)排序,得到\(b_i\),记录\(c_i\)为\(b_i\)在原序列中的位置,即\(a_{c_i}=b_i\)。
满足题意的排序的总数是\(\prod_{i=1}^n b_i-i+1\),有非正数就是0。提前判掉。
考虑枚举一对\((i,j),i<j\),那么有\(b_i\le b_j\),计算他们的贡献:
如果\(c_i<c_j\),则要想产生逆序对两者只有\(\binom{b_i-i+1}{2}\)种取值。贡献为
\[ \binom{b_i-i+1}{2}\prod_{k=1}^{i-1}b_k-k+1\prod_{k=i+1}^{j-1}b_k-k\prod_{k=j+1}^nb_k-k+1 \newline =\frac{b_i-i}{2(b_j-j+1)}\prod_{i=1}^nb_k-k+1\prod_{k=i+1}^{j-1}\frac{b_k-k}{b_k-k+1} \]
这个很好计算,倒着枚举\(i\),维护所有\(j\)的答案就可以了。注意那个区间乘积不能用前缀积维护,因为有可能有0导致前缀积会出现零除以零的情况。
如果\(c_i>c_j\),那么\(j\)的取值范围更大,而且\(j\)在序列中排在 \(i\)前面。与上面的情况不同之处在于,此时不仅有上面\(\binom{b_i-i+1}{2}\)的贡献,\(p_j\)还可以取\((b_i,b_j]\),这部分要单独算。枚举\(p_j\)的取值\(t\),可知这部分贡献是
\[ \sum_{t=b_i+1}^{b_j}\prod_{k=1}^{i}b_k-k+1\prod_{k=i+1}^{j-1}b_k-k+[t>b_k]\prod_{k=j+1}^nb_k-k+1 \newline =\frac{\prod_{k=1}^nb_k-k+1}{b_j-j+1}\sum_{t=b_i+1}^{b_j}\prod_{k=i+1,b_k\ge t}^{j-1}\frac{b_k-k}{b_k-k+1} \]
这个考虑枚举\(j\),以\(c_i\)为下标维护所有\(i\)的贡献,方便用数据结构求和。我们把每一坨\(\prod_{k=i+1,b_k\ge t}^{j-1}\frac{b_k-k}{b_k-k+1}\),扔在\(c_i\)的位置,最开始扔的时候只是扔一个1,后面考虑当\(j\rightarrow j+1\)时的改变:对于所有\(i<j+1\)对应的\(c_i\)值,旧有的贡献都要乘上\(\frac{b_j-j}{b_j-j+1}\),然后再额外加上\(b_{j+1}-b_j\)个1,也就是\(+=b_{j+1}-b_j\)。可以用线段树维护,需要实现对激活点区间加,激活点区间乘,激活一个点的操作。
f
比e简单,但我还是不会做
我想到了个大概,但是完整的策略拿不出来,真傻逼。
这个题要维护块。最开始每个点自己成一个块。把所有的块(最开始就是所有的点)扔进一个set里面,按照\(\frac{cnt_1}{cnt_0}\)排序(注意要写一个结构体维护,\(cnt_0\)可能是0)。 然后取set中最小的元素,如果这个点父亲已经没了,表示这个点现在可以用了。那么直接把这个块加入答案中。
如果这个点父亲还在,说明这个点很优,但是被父亲压住了,父亲被选完后应该立即选这个点。因此,把这个点和父亲合并,更新父亲点重新扔进set里面。
重复以上操作直到set为空。
agc024
a
k%2==0?A-B:B-A
b
设\(pos[p[i]]=i\),pos[]最长的递增连续子串长度是m,Ans=n-m。
c
假设你想要得到一个\(X[i]=a[i]\),\(X[i-1]\)就至少要变成\(a[i]-1\),\(X[i-2]\)就至少要变成\(a[i]-2\),.....
注意到\(X[i]\)变大了就没法再变小。因此上面可以作为一个判无解的依据
然后再理性分析一下,就大概知道倒着扫一遍就完了:
倒着扫,维护一个值cur表示\(X[i]\)至少得是多少。如果遇到\(a[i] < cur\),直接无解。如果遇到\(a[i]==cur\),说明为了达到后面的某个\(a[i']\),\(X[i]\)已经变成\(a[i]\)了,什么都不用干。如果\(a[i]>cur\),说明\(a[i]\)需要从0构建上来,因此\(ans+=a[i],cur=a[i]\)。每次循环起始将\(cur--\)。
d
居然切了一道1100,我焯,难道我真是天才
首先不难想到最好应该是把整棵树弄成一个非常对称的结构,选定一个点或者一条边为根后整棵树相同深度的点都可以标成同样的颜色。因此,考虑先求出树的直径上点数\(d\),然后所求的最小\(\text{colorfulness}\)就是\(\frac{d+1} 2\)。
然后求第二个答案也很简单。比如如果有一个点下面10个叶子,那么所有的\(\text{maxdepth}-1\)的点都至少要挂10个叶子。这样扫一遍,记录相同深度最多的儿子个数,答案就是一个累乘。
需要注意的是数的直径不止有一条,需要枚举所有的中间点或中间边为根。还需要注意,\(d\)是奇数并不意味着最后的树一定是以一个点为根,也可能是以一条边为根。参见样例2。
e
不会。最开始一直想错方向了,想到单调栈上面去了想不明白
观察这个操作,要保证插入一个数之后字典序变大,就必须要满足序列的下一个与你插入的数不同的数比你插入的数小
注意到,如果后面有一串数与你当前插入的数相同,考虑把你当前插入的数直接挪到后面的第一个不一样的数前面,过程是等效的,所以为了去重和便于计算,可以直接假定你插入的数必须比下一个数严格大。
然后通过整个插入的过程可以构建一棵树:每个点有一个标号代表这个点是第几次插入的,还有一个权值表示这次插入的数是多少。最开始只有一个点(0,0)表示序列的结尾。然后插入一个新点的时候,就把他挂在他后面的那个比他严格小的数下面。那么这棵树要满足的条件就是每个点的标号和权值都严格大于父亲。可以看出这棵树和题目所求tuple序列有一一映射:显然序列一一映射到树,而对于一棵树倒着来,每次把标号最大的点取出来,结合上面已经给相等的数定了序,这样就能一一映射到一个序列。因此只需要对树计数。
树的计数相对简单,考虑dp。假设\(f_{i,j}\)表示大小为\(i\)的树已经标号,根节点的权值是\(j\)的树有多少种。转移方程\(f_{i,j}=\sum_{x=1}^{i-1}\sum_{y=j+1}^{k}f_{x,y}\times f_{i-x,j}\times\binom{i-2}{x-1}\),直接做是\(O(n^2k^2)\)的,可以用前缀和优化掉\(\sum_{y=j+1}^k\)的这层循环,\(O(n^2k)\)。
f
想了半个小时没有任何想法
这个题是怎么做到构造这么简单,这么好理解但是这么难的
考虑建一个dag,这个dag满足:
有红,黑,蓝三种点
每个长度小于等于n的串对应了一个红点和一个蓝点
假如a是b的子序列,那么有且仅有一条从b的红点到a的蓝点的路径,否则没有这样的路径
先考虑如何判断a是不是b的子序列。用贪心的想法维护每个字串的子序列集合。某个序列,比如1110001的子序列集合[1110001]可以划分成三种:
子序列第一个位置是1,这类可以表示为1[110001]
子序列第二个位置是0,这类可以表示为0[001]
子序列是空串
然后这样形如x[y]\(\to\)x0/1[y去掉最高的0/1]的转移形成一个dag。a是b的子序列当且仅当[b]可以走到a[...]这种点。并且如果能,这种走法是唯一的。
然后我们考虑利用这个转移做如下建图
对于len(x)+len(y)<=n的两个串x,y,建立黑点x[y]
如果y有1,把x[y]连向x1[y去掉第一个1和前面的部分]
如果y有0,把x[y]连向x0[y去掉第一个0和前面的部分]
对每个串x建立红点[x],连向黑点[x]
对每个串x建立蓝点x[],由所有黑点x[...]连向它
然后跑dp,然后就能算出每个串是多少个串的子串,然后for一遍算答案。复杂度\(O(n2^n)\)。